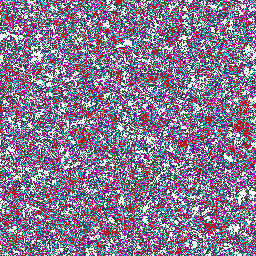Gaussian and Clipped Gaussian Random Fields
|
The graphics on this page is based on the PhD thesis of
(1) Boris Kozintsev, 1999. Images of isotropic Gaussian
random fields (mean 0, variance 1) and their clipped versions
can be generated on-line using software created by
>
(2) Boris Kozintsev, 1999. The on-line implementation
requires a correlation structure (4 choices are available; an
additional is custom-built),
correlation parameters,
field size (e.g. 256 by 256), desired output format, and some
clipping information.
Clipped Gaussian random fields can be used for modeling discrete-valued
random fields with a given correlation structure. If every
quantization level is represented by a specific color, then clipping
at several levels produces
a color map. Note that in "cgi?3" there are 3 colors, in
"cgi?9" there are 9 colors, etc.
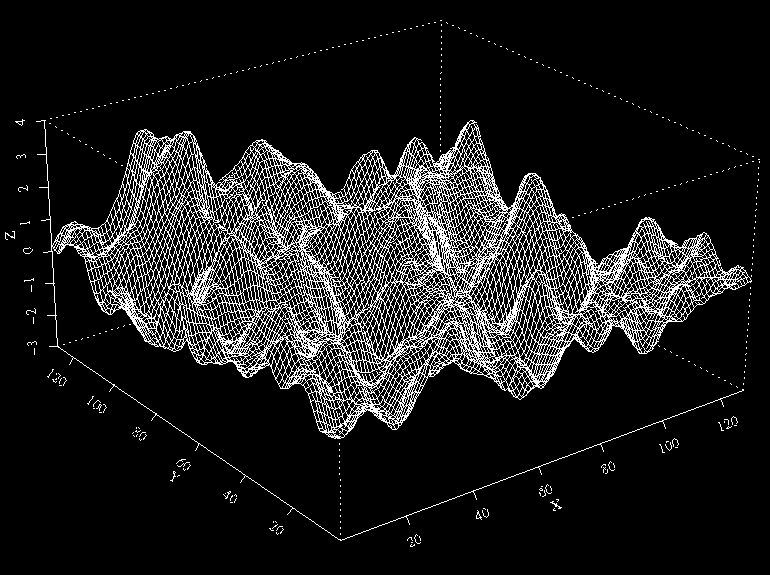
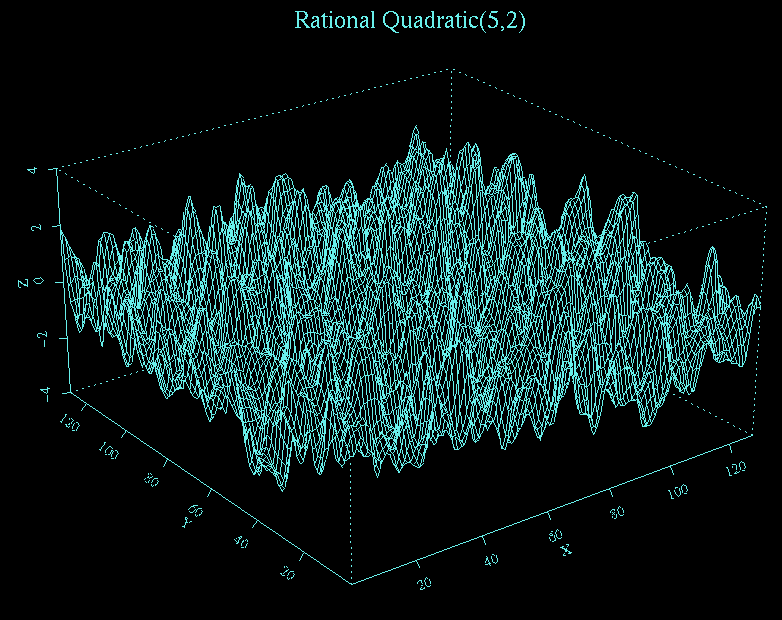
The following S-Plus image is a 128 by 128
realization of an isotropic Gaussian field with Matern correlation with
parameters 5 and 2. The 3D data for similar images for a given
isotropic correlation function can be
generated on line in the form of triplets (x,y,z) or just
the z coordinate, as needed.
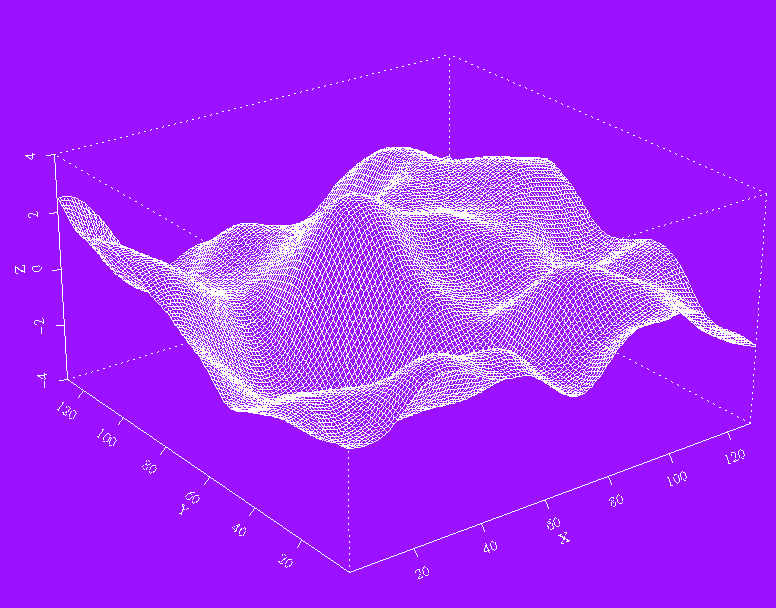
A mixure of red and blue adds some color to 128 by 128
Matern(5,5), still using S-Plus,
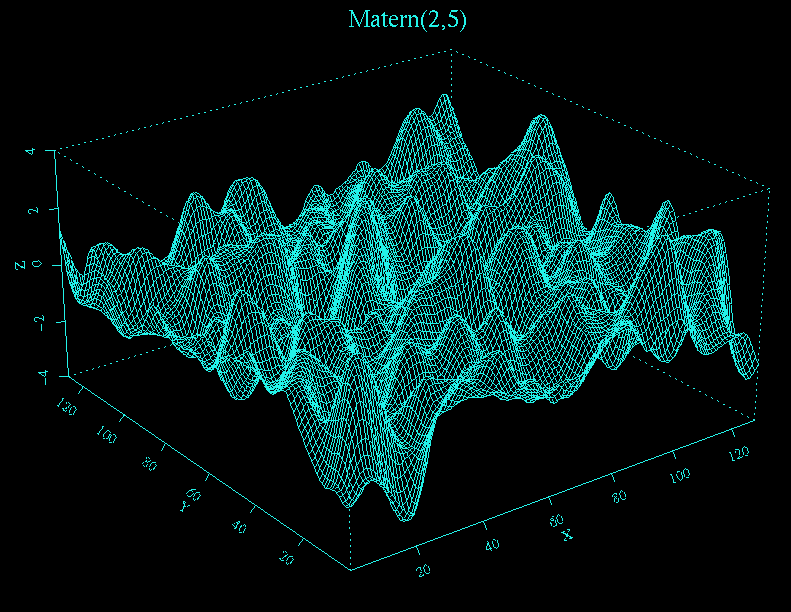
Matern(2,5) 128b 128 realization plotted with S-Plus looks like this,
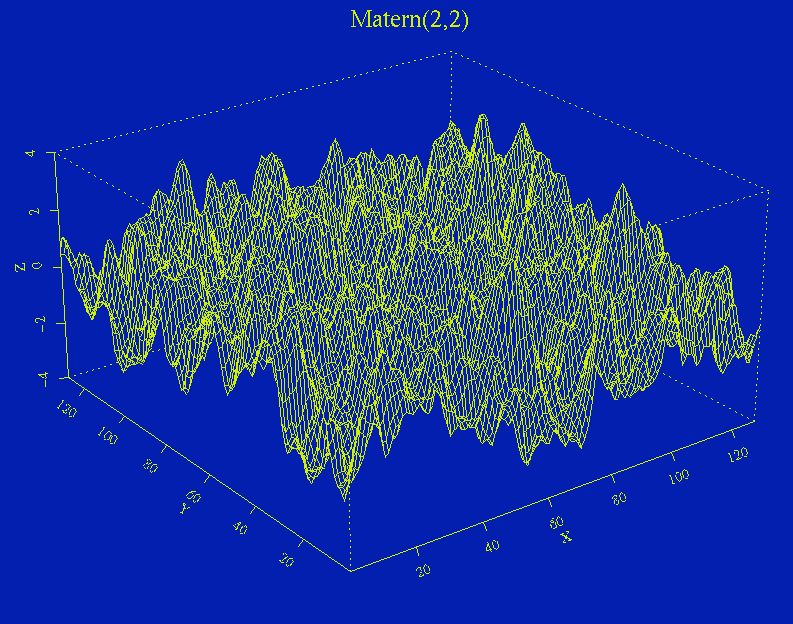
A rougher surface is obtained with Matern(2,2) correlation,
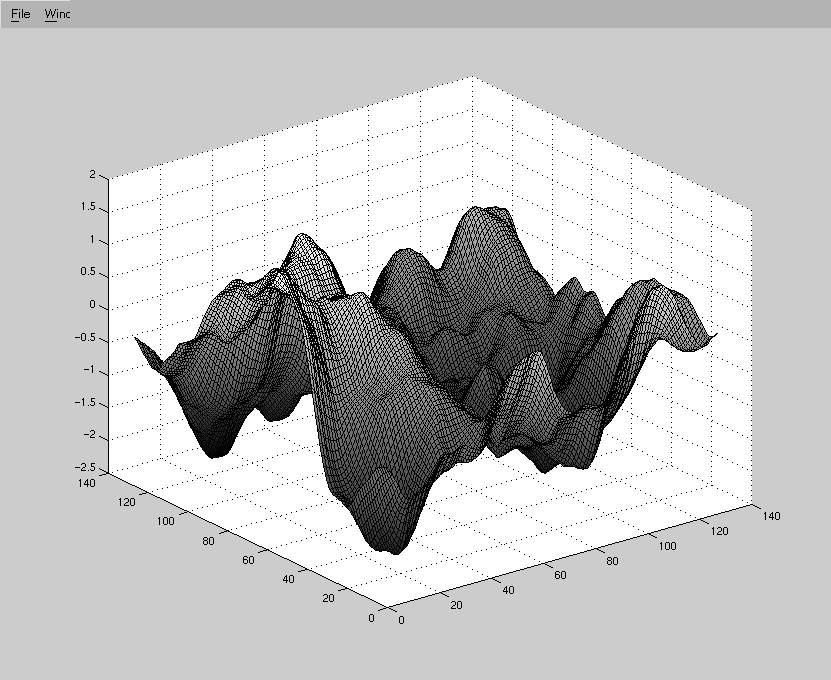
Switching to Matlab,
here is a 128 by 128 realization with Matern(11,2)
correlation function plotted with Matlab,
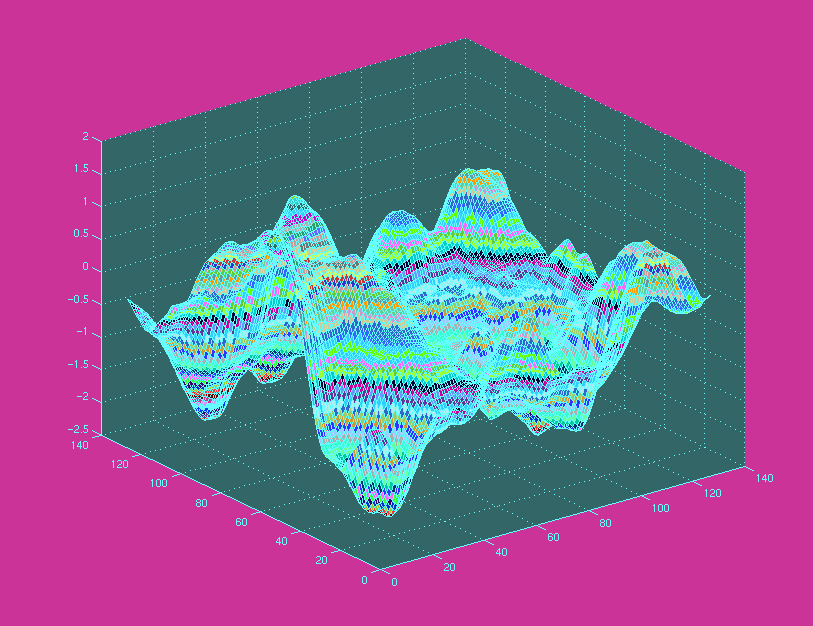
The same with random coloring,
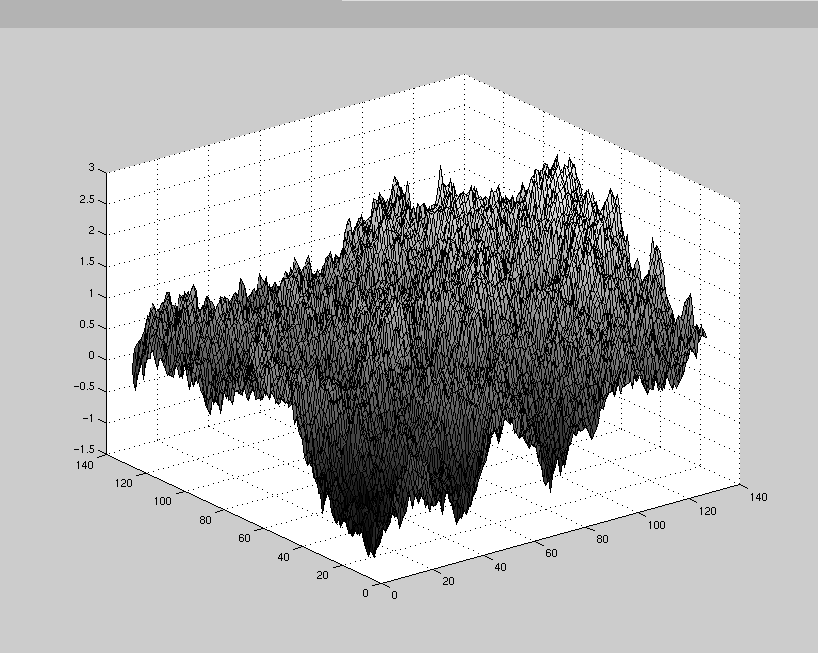
Realizations with spherical correlation function tend to be more
oscillatory as the following 128 by 128 image with correlation parameter
120.
Next is even a rougher 128 by 128 realization from an exponential
correlation function with parameters 0.8 and 1.6.
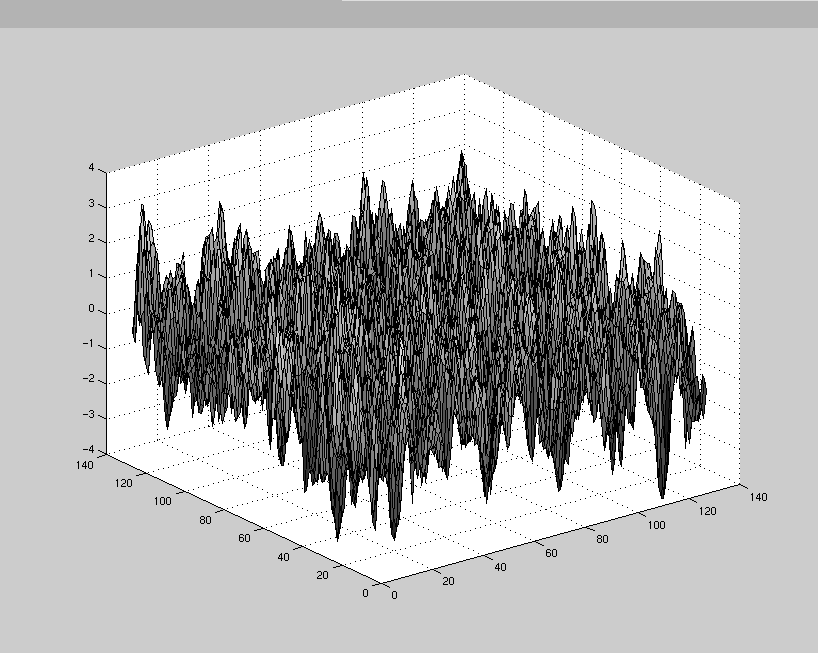
A 128 by 128 realization from a rational quadratic
correlation function with parameters 4 and 2 looks like this:
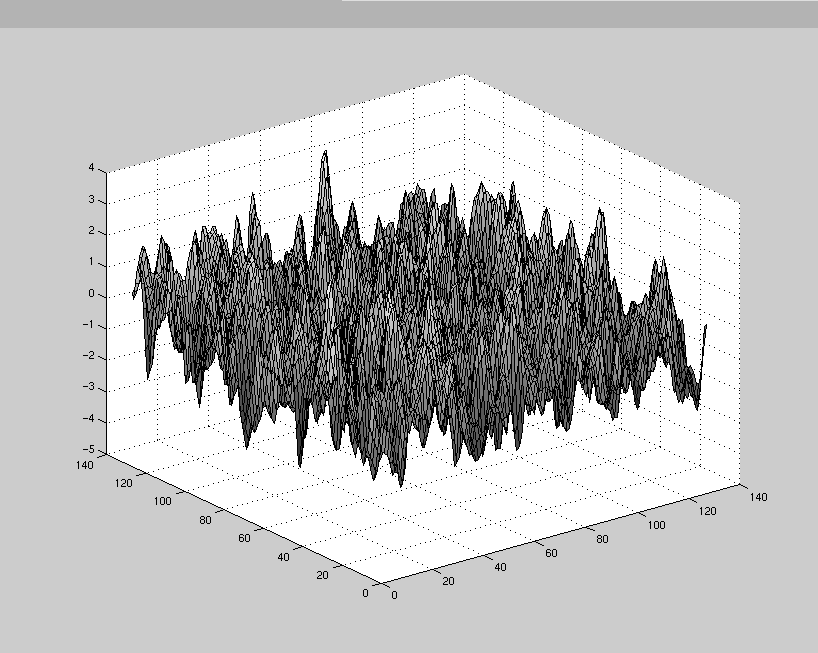
Put some color on a 128 by 128 realization from a rational quadratic
correlation function with parameters 5 and 2, reverting to S-Plus,
Clipping--or quantization--at several levels provides
an alternative way to visualize a random field.
The following color
maps were obtained by clipping at several
levels a 256 by 256 Gaussian field with isotropic Matern
correlation with
parameters 7 and 4, rational quadratic correlation with
parameters 10 and 7, and rational quadratic correlation with
parameters 2 and 1, respectively.



Similarly, the next triplet pertain to spherical
correlation with parameter 50, exponential correlation with
parameters .5 and .9, and Matern correlation with parameters
7 and 2 at 10 levels, respectively.

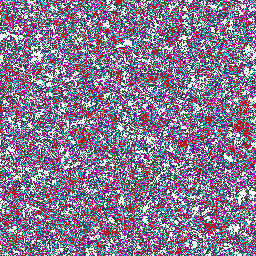

The following clipped images were obtained from three
realizations of an isotropic
Gaussian random field with spherical correlation with parameter
100.



The next clipped images were obtained from different
realizations of an isotropic Gaussian random field with Matern
correlation with parameters 0.9 and 1.9.



Next is a triplet of clipped images corresponding to
Matern(5,2), spherical(5), and rational quadratic(5,2).



Next is a triplet of clipped
images--statistically identical--corresponding to
spherical(77). 6 colors: light green, orange, magenta, white,
cyan, and forest green.



Three clipped iamges, 256 by 256, Matern(5,4), 7 colors: orange,
magenta, cyan, dark blue, light blue, forest green, yellow.



Some 256 by 256 binary images with exponential(.8,2) correlation,


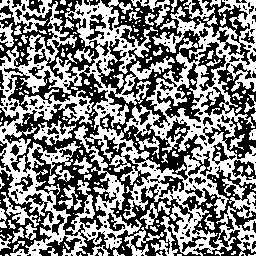
Two 300 by 300 images corresponding to spherical(17). 8
colors: dark blue, yellow, brown, magenta, light green, forest
green, orange, red, at 12.5% each.


Finally, 12 independent images from spherical(120), 5 colors
(orange, light green, magenta, white, cyan) at 20% each,
each of scaled size 256 by 256.