Lines, Planes and MATLAB

Example 1:
Example 2:
Example 3:
Example 4:
Problem 1:
Problem 2:

In this published M-file, we will use MATLAB to solve problems about lines and planes in three-dimensional space. The mathematical content corresponds to chapter 11 of the text by Gulick and Ellis.

We begin with the problem of finding the equation of a plane through three points.

Example 1:

Find an equation for the plane through the points (1,-1,3), (2,3,4), and (-5,6,7).

We begin by creating MATLAB arrays that represent the three points:

P1 = [1,-1,3];
P2 = [2,3,4];
P3 = [-5,6,7];

If you wish to see MATLAB's response to these commands, you should delete the semicolons. Next, we create the normal vector to our plane by taking the cross-product of two vectors parallel to the plane.

normal = cross(P1-P2, P1-P3)

normal =

     9   -10    31

Next, we declare x, y, and z to be symbolic variables, create a vector whose components represent the vector from P1 to a typical point on the plane, and compute the dot product of this vector with our normal.

syms x y z
P = [x,y,z]
planefunction = dot(normal, P-P1)

 
P =
 
[ x, y, z]
 
 
planefunction =
 
9*x - 10*y + 31*z - 112

The equation of our plane is now planefunction = 0. We remark that the MATLAB's symbolic dot product assumes that the its arguments may be complex and takes the complex conjugates of the components of its first argument. To see the effect of this, we compute instead:

dot(P-P1, normal)

 
ans =
 
9*conj(x) - 10*conj(y) + 31*conj(z) - 112

Since in this course we only want dot products of real-valued vectors, it helps instead to define

realdot = @(u, v) u*transpose(v);

to avoid this annoyance.

realdot(P-P1,normal)

 
ans =
 
9*x - 10*y + 31*z - 112

Example 2:

Let us now use the equation of the plane in Example 1 to find the point of intersection of the plane with the line through (1,2,-1) and (3,3,3).

P4 = [1,2,-1];
P5 = [3,3,3];

We parametrize the line:

syms t
line = P4 + t*(P5-P4)

 
line =
 
[ 2*t + 1, t + 2, 4*t - 1]

line now gives the coordinates of a typical point on our line in terms of the parameter t. We can now evaluate planefunction at such a point by substituting line for P.

newfunction = subs(planefunction, P, line)

 
newfunction =
 
132*t - 154

Now we solve newfunction = 0 for t, and substitute the result in line to obtain our desired point, and check our answer.

t0 = solve(newfunction)
point = subs(line, t, t0)
subs(planefunction, P, point)

 
t0 =
 
7/6
 
 
point =
 
[ 10/3, 19/6, 11/3]
 
 
ans =
 
0

Notice that the command solve(newfunction) automatically sets the function to zero, recognizes the independent variable, and solves for it.

Example 3:

Let us now use the plotting capabilities of MATLAB to plot the plane and the line. First we solve for z in terms of x and y in the equation of the plane.

zplane = solve(planefunction, z)

 
zplane =
 
(10*y)/31 - (9*x)/31 + 112/31

We will now plot our plane and our already parametrized line on the same set of axes. We will use the command hold on to put both plots on the same diagram.

ezplot3(line(1), line(2), line(3), [-1,3]), hold on
ezmesh(zplane, [2, 8, 2, 8]), hold off
axis([2, 8, 2, 8, 0, 6]), title ''

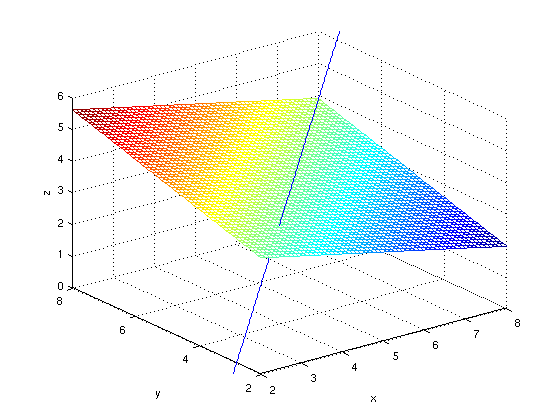
We should point out that doing things this way with ezmesh and ezplot3, it's necessary to plot first the line and then the plane. The reason is that the code for ezplot3 is written in such a way as to undo the effect of any previously issued hold on command. Of course one can get around this by using plot3 instead of ezplot3, like this:

ezmesh(zplane, [2, 8, 2, 8]), hold on
tt = -1:3;
linex = subs(line(1), t, tt);
liney = subs(line(2), t, tt);
linez = subs(line(3), t, tt);
plot3(linex, liney, linez), hold off
axis([2, 8, 2, 8, 0, 6]), title ''

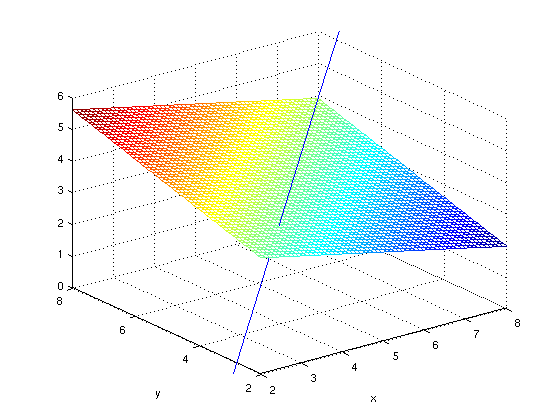
But obviously this is more awkward.

Example 4:

Let us now see if we can find an equation for the cylinder of radius 3 around our line (Compare Gulick and Ellis Section 11.5 Problem 26). The cylinder in question is the set of all points whose distance from the line is 4. P already represents a generic point with coordinates (x,y,z) and line represents a point on the line. Thus the square of the distance from a point in space to a point on the line is given by

distsq = realdot(P-line, P-line)

 
distsq =
 
(t - y + 2)^2 + (z - 4*t + 1)^2 + (2*t - x + 1)^2

What we want to do is to minimize this squared distance as a function of t, while keeping x, y, and z generic.

distsqprime = diff(distsq, t)
tcrit = solve(distsqprime, t)
distsqfunc = simplify(subs(distsq, t, tcrit))
cylinder = distsqfunc - 9

 
distsqprime =
 
42*t - 4*x - 2*y - 8*z
 
 
tcrit =
 
(2*x)/21 + y/21 + (4*z)/21
 
 
distsqfunc =
 
((8*x)/21 + (4*y)/21 - (5*z)/21 - 1)^2 + ((2*x)/21 - (20*y)/21 + (4*z)/21 + 2)^2 + ((2*y)/21 - (17*x)/21 + (8*z)/21 + 1)^2
 
 
cylinder =
 
((8*x)/21 + (4*y)/21 - (5*z)/21 - 1)^2 + ((2*x)/21 - (20*y)/21 + (4*z)/21 + 2)^2 + ((2*y)/21 - (17*x)/21 + (8*z)/21 + 1)^2 - 9

Setting the last output to 0 gives us a function for the cylinder.

Problem 1:

In this problem you will find the distance from point P4 to the plane of Example 1 three different ways:

(a) By using the method of Section 11.6 of Gulick and Ellis, performing the calculations with MATLAB.
(b) By finding the foot of the perpendicular from P4 to the plane as follows:

Parametrize the line through P4 normal to the plane.
Find the point common to the line you have just parametrized and the plane, as in Example 2.
Find the distance between the point you have just found and P4.

Verify that methods a) and b) give the same answer.

(c) By parametrizing the plane and minimizing the square of the distance from a typical point on the plane to P4. Parametrize the plane in the form P1+s(P2-P1)+t(P3-P1). As in Example 4, find and name the distance from P4 to a typical point on the plane. Still as in Example 4, but retaining s as a parameter, minimize the square of the distance with respect to t. The result should still contain the parameter s. Then minimize the result with respect to s.

Problem 2:

Find the equation of the plane in Example 1 in another way, by assuming that the equation has the form ax + by + cz = 1 (this is always possible if the plane doesn't go through the origin), and solving for a, b and c so as to make the plane pass through P1, P2, and P3. Check that your answer agrees with the one we found above.