Triple Integrals

copyright © 2000 by Paul Green and Jonathan Rosenberg

Evaluating Triple Iterated Integrals

In passing from double to triple integrals, there is much less that is novel than in passing from single to double integrals. One practical difference, however, is that MATLAB has no built-in triple integrator. (In other words, there is no trplquad similar to dblquad.) However, threefold iterated integrals can be formulated and evaluated using the symbolic toolbox's MAPLE routines, in the same manner as twofold iterated integrals. And if the first of the three integrals can be evaluated symbolically, it is then possible to use dblquad for the remaning integrations.

Example 1:

We will begin by considering the iterated integral . We can evaluate this easily as

syms x y z

firstans=int(int(int(x*y*z,z,0,3-x-y),y,0,3-x),x,0,3)

firstans =

81/80

We can also evaluate the first integral only, and then use dblquad or numint2 for the remaining two integrations:

f=int(x*y*z,z,0,3-x-y)

f =

1/2*x*y*(3-x-y)^2

secondans=numint2(f,y,0,3-x,x,0,3)

Warning: Recursion level limit reached in quad. Singularity likely.

> In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 102

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 141

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 141

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 141

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 141

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 142

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 142

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 142

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 142

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 142

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m (quadstp) at line 142

In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m at line 72

In C:\MATLABR12B4\toolbox\matlab\funfun\@inline\feval.m at line 15

In C:\MATLABR12B4\toolbox\matlab\funfun\dblquad.m at line 60

In E:\class\math241\common\numint2.m at line 17

Warning: Recursion level limit reached 16 times.

> In C:\MATLABR12B4\toolbox\matlab\funfun\quad.m at line 80

In C:\MATLABR12B4\toolbox\matlab\funfun\@inline\feval.m at line 15

In C:\MATLABR12B4\toolbox\matlab\funfun\dblquad.m at line 60

In E:\class\math241\common\numint2.m at line 17

secondans =

1.0125

Although the four places shown happens to coincide exactly with the first answer, the numerical procedure did not, in fact, give precisely that value:

double(firstans-secondans)

ans =

4.2016e-006

We have also written a purely numerical triple integrator, oldnumint3, with syntax analogous to numint2. But because dblquad is so slow (and the same algorithm extrapolated to three dimensions would be even slower), we have looked for an alternative, based on a freeware package of M-files called the numerical integration toolbox. This toolbox is much faster and more adaptable (though admittedly sometimes harder to use) than dblquad. We have installed this package in a subdirectory called nit. To use it, first add the package with the command:

addpath nit

(Depending on your set-up, you may need to edit this to an absolute pathname.)

To see how it works, we first try out an alternative version of numint2, based on nit, called newnumint2. The syntax is the same as for numint2, but there is an optional final parameter, which is the number of subdivision points to use in each direction. (The default is 20.) The higher this parameter, the more accurate the results; however, the running time of the algorithm is proportional to the square of this parameter, so be careful about increasing it.

thirdans=newnumint2(f,y,0,3-x,x,0,3)

thirdans =

1.0125

Note that this answer looks the same as the first two to four decimal places, but that we are spared all the annoying warning messages. The accuracy is:

double(firstans-thirdans)

ans =

0

which is pretty good!! Now we try a totally numerical integration. The analogue of newnumint2 for triple integrals is called numint3. Again there is an optional final parameter, which is the number of subdivision points to use in each direction. (The default is 8.) The higher this parameter, the more accurate the results; however, the running time of the algorithm is proportional to the cube of this parameter, so be extra careful about increasing it.

fourthans=numint3(x*y*z,z,0,3-x-y,y,0,3-x,x,0,3)

fourthans =

1.0125

The accuracy is:

double(firstans-fourthans)

ans =

0

Again pretty good!

Problem 1: Evaluate the threefold iterated integral 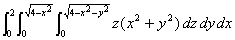, both symbolically and numerically. (For the numerical integration, first do the integral over z, then use newnumint2 on this intermediate result.)

Finding the Limits

The remaining issue in the evaluation of triple integrals is the determination of limits. Once this has been done, the actual integration can always be performed by one of the methods illustrated above.

Example 2:

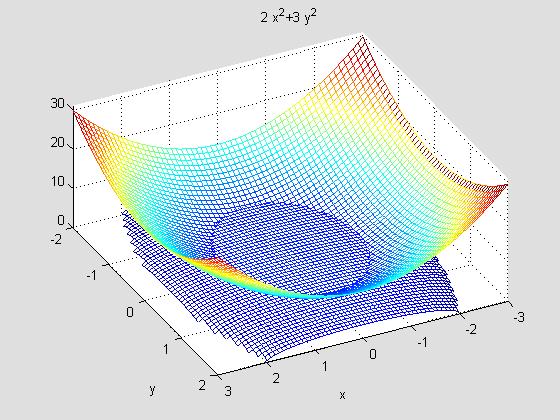
Let us consider the region above the paraboloid z = 2x² + 3y² and inside the ellipsoid 3x² + 2y² +z² = 20. We might begin by plotting the two surfaces simultaneously. Since z is never negative on or above the paraboloid, we are interested only in positive vaues of z. Consequently, we will solve the equation of the ellipsoid for positive z and use ezmesh to plot both surfaces.

ezmesh(sqrt(20-3*x^2-2*y^2),[-3,3,-2,2]);

hold on

ezmesh(2*x^2+3*y^2, [-3,3,-2,2])

view([1,2,3])

hold off;

From the viewpoint we have chosen, using MATLAB's view comand, we can see that there is a region inside the ellipsoid that is bounded below by the paraboloid and above by the ellipsoid. This determines the lower and upper limits for z. Accordingly, we set

z1=2*x^2 + 3*y^2

z2=sqrt(20-3*x^2-2*y^2)

z1 =

2*x^2+3*y^2

z2 =

(20-3*x^2-2*y^2)^(1/2)

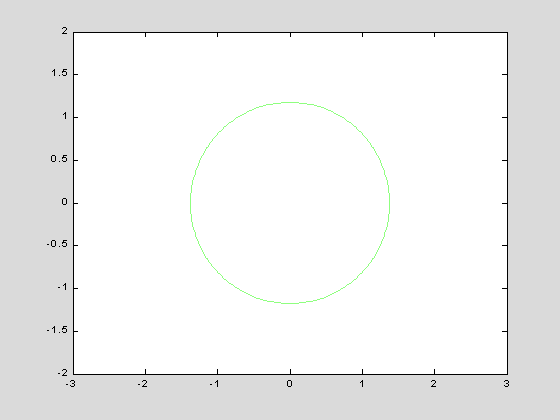
To determine the limits for x and y, it may be helpful to plot the curve along which the upper and lower limits for z coincide. We will do this using genplot's contour option:

genplot(z2-z1,-3:.05:3,-2:.05:2,'contour',[0,0])

Although this looks like an ellipse, it is actually a quartic curve. We will establish the limits by solving the equation of the curve for y as a function of x. We expect two solutions, corresponding to the upper and lower y limits, and we should be able to determine the x limits by setting the y limits equal to each other.

ylims=solve(z2-z1,y)

ylims =

[ 1/3*(-1-6*x^2+(181-15*x^2)^(1/2))^(1/2)]

[ -1/3*(-1-6*x^2+(181-15*x^2)^(1/2))^(1/2)]

[ 1/3*(-1-6*x^2-(181-15*x^2)^(1/2))^(1/2)]

[ -1/3*(-1-6*x^2-(181-15*x^2)^(1/2))^(1/2)]

solve has found four solutions instead of two. This should not surprise us too much since the equation in question is quartic. If we look carefully, we can see that the last two solutions involve square roots of negative quantities, so that the limits we want are the first two. However, we want the first one to be the upper limit and the second to be the lower limit so we set

y1=ylims(2)

y2=ylims(1)

y1 =

-1/3*(-1-6*x^2+(181-15*x^2)^(1/2))^(1/2)

y2 =

1/3*(-1-6*x^2+(181-15*x^2)^(1/2))^(1/2)

xlims=solve(y2-y1,x)

xlims =

[ 1/4*(-6+2*329^(1/2))^(1/2)]

[ -1/4*(-6+2*329^(1/2))^(1/2)]

x1=double(xlims(2))

x2=double(xlims(1))

x1 =

-1.3756

x2 =

1.3756

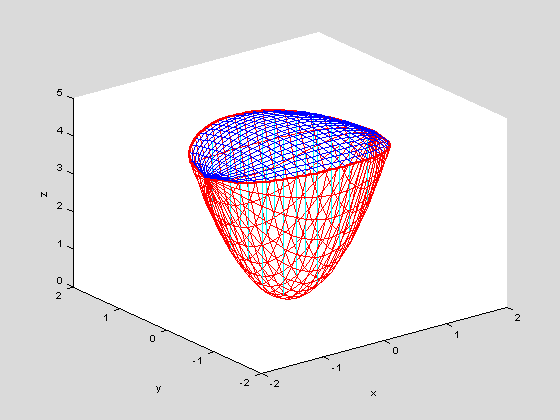
We can now check our limits for geometric plausibility. For this purpose we have written an m-file called viewSolid. It takes a proposed set of limits of integration (written from the inside to the outside) and draws a picture of the corresponding region.

viewSolid(z,z1,z2,y,y1,y2,x,x1,x2)

This looks reasonable; we may now use the limits we have found to integrate any function we like over the region in question.

Problem 2: Find the appropriate limits for integrating over the region bounded by the paraboloids z = 3x² + 4y² and z = 9-x²-5y². Check your results using viewSolid.

What is special about the examples we have just considered is that the region in question is bounded by two surfaces, each of which has an equation specifying z as a function of x and y. The procedure we have used in this case will work for any such region, as long as solve is able to solve the associated equations. We will look now at an example of another sort.

Example 3:

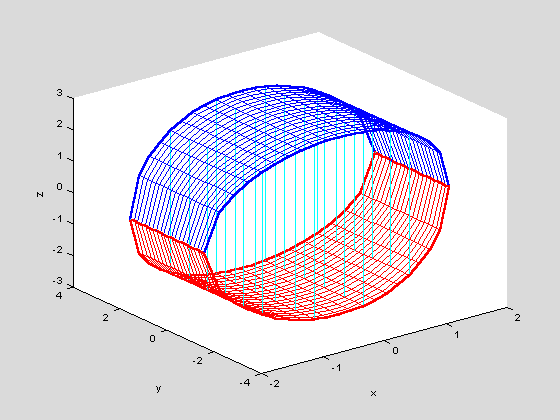
We consider the region interior to both of the elliptical cylinders, x^2+2y^2 = 9 and 2x^2+z^2 = 8. We begin by observing that the condition that a point be interior to both cylinders constrains x^2 to be at most 4. We also observe that, for fixed x, the limits for y and z are determined independently of each other. So we'll want to put the x-integral on the outside. We can immediately set

x1=-2; x2=2;

y1=-sqrt((9-x^2)/2); y2=-y1;

z1=-sqrt(8-2*x^2); z2=-z1;

We can again use viewSolid to check the plausibility of these limits, although the resulting plot is more difficult to interpret in this case, since it shows only the upper and lower boundaries as surfaces; the side boundaries are shown as ensembles of vertical lines.

viewSolid(z,z1,z2,y,y1,y2,x,x1,x2)

Problem 3: Find limits appropriate for integrating over the solid region bounded by the paraboloid y = x² + z²-2 and the cylinder x² + y² = 1. Check your results with viewSolid.

Additional Problems:

1. Find the volume of each of the solid regions considered in Examples 2 and 3 and Problems 2 and 3 above. Use at least two different methods in each case and compare the answers.

2. Integrate the function x² + y*z over the solid region above the paraboloid z = x² + y² and below the plane x + y + z = 10.

3. Integrate the function x² + 2y² + 3z² over the solid region interior to both the sphere

x² + y² + z² = 9 and the cylinder (x-1)² + y² = 1.