Solving a 2nd order ODE with the Improved Euler method

Contents

Initial value problem

We consider an initial value problem for a 2nd order ODE:

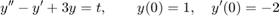
$$y''-y'+3y=t,\qquad y(0)=1,\quad y'(0)=-2$$

and we want to find the solution y(t) for t in [0,4].

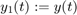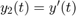We first have to rewrite this as a 1st order system: Let $y_1(t):=y(t)$ and $y_2(t)=y'(t)$, then we obtain

$$\left[\begin{array}{c}y_1' \\ y_2'\end{array}\right] = \left[\begin{array}{c}y_2 \\ t+y_2-3y_1\end{array}\right], \qquad \left[\begin{array}{c}y_1(0) \\ y_2(0)\end{array}\right] = \left[\begin{array}{c} 1\\ -2\end{array}\right]$$

Now we can define a vector valued function f(t,y) and an initial vector y0.

We use ode45 to find the solution of the initial value problem. At the final time T we obtain the approximation yfin = [y1fin,y2fin] for $[y(T),y'(T)]$.

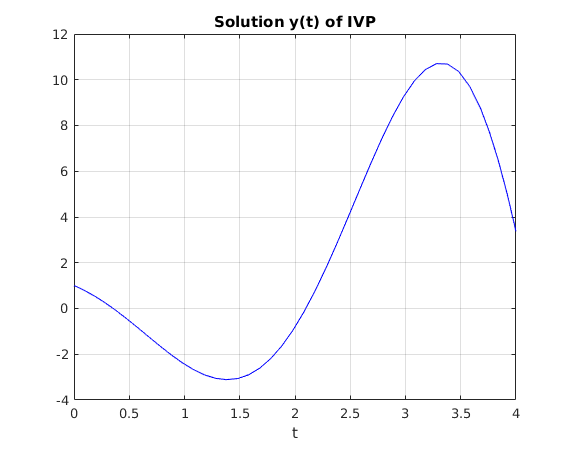
We plot the solution 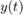$y(t)$.

function Ieuler_demo2

f = @(t,y) [y(2); t+y(2)-3*y(1)]; % define function f(t,y)
t0 = 0;  y0 = [1;-2];             % initial condition with vector y0
T = 4;                            % final t-value
[ts,ys] = ode45(f,[t0,T],y0);     % solve IVP

yfinal = ys(end,:);               % approximations for y1(T),y2(T)

fprintf('y(T) = %g, y''(T) = %g\n',ys(end,1),ys(end,2))

plot(ts,ys(:,1),'b'); hold on     % plot solution y(t)
title('Solution y(t) of IVP')
xlabel('t'); grid on

y(T) = 3.36902, y'(T) = -21.7257

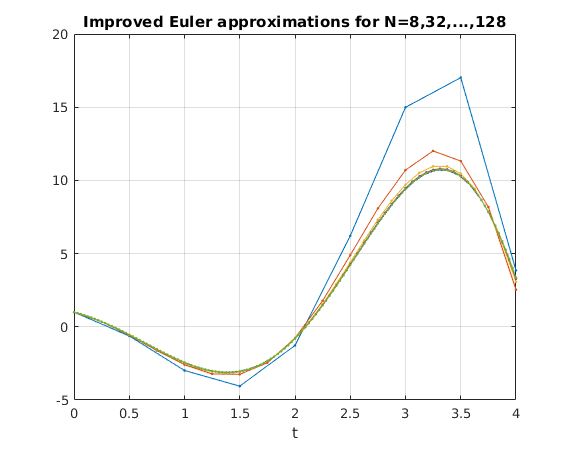
Use Improved Euler method with N=8,16,32,...,128

We see that the Euler approximations get closer to the correct value as N increases.

When we double the value of N the error gets divided by about 4. This means that the error is bounded by 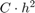$C\cdot h^2$: The Euler method converges with order $h^2$.

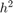olderr = NaN;
for N = 2.^(3:7)
  [ts,ys] = IEuler(f,[t0,T],y0,N);
  err = norm(ys(end,:)-yfinal);    % norm of error
  fprintf('N = %3g, y(T) = [%10g,%10g], ||error|| = %10g, quotient = %g\n',N,ys(end,:),err,olderr/err)
  olderr = err;
  plot(ts,ys(:,1),'.-')            % plot Euler approximaton for y1 (1st column of ys)
end
hold off
title('Improved Euler approximations for N=8,32,...,128')

N =   8, y(T) = [   3.84777,  -44.0519], ||error|| =    22.3314, quotient = NaN
N =  16, y(T) = [    2.5381,  -26.9189], ||error|| =    5.25928, quotient = 4.2461
N =  32, y(T) = [   3.07319,  -22.9907], ||error|| =    1.29912, quotient = 4.04833
N =  64, y(T) = [   3.28324,  -22.0368], ||error|| =   0.322733, quotient = 4.02538
N = 128, y(T) = [   3.34614,  -21.7992], ||error|| =  0.0770437, quotient = 4.18896

Code of function IEuler(f,[t0,T],y0,N)

At each step we evaluate the slope twice: first at the current point, then at the Euler approximation. We then use the mean (s1+s2)/2 to find the new y value.

function [ts,ys] = IEuler(f,tv,y0,N);
  t0 = tv(1); T = tv(2);
  h = (T-t0)/N;                    % stepsize h
  ts = zeros(N+1,1); ys = zeros(N+1,length(y0));
  t = t0; y = y0;                  % initial point
  ts(1) = t; ys(1,:) = y';

  for i=1:N
    s1 = f(t,y);                   % evaluate direction field at current point
    yE = y + s1*h;                 % find Euler value yE
    s2 = f(t+h,yE);                % evaluate direction field at Euler point
    y = y + (s1+s2)/2*h;           % use mean (s1+s2)/2 to find new y
    t = t + h;
    ts(i+1) = t; ys(i+1,:) = y';   % store y(1),y(2) in row of array ys
  end
end

end


Published with MATLAB® R2017a