How to compute y=1-cos(x) for x=2*10^(-6)

Contents

Unavoidable error

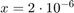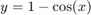For $x=2\cdot 10^{-6}$ compute $y=1-\cos(x)$.

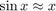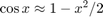The condition number is (using Taylor approximations $\sin x\approx x$ and $\cos x\approx 1-x^2/2$)

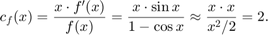
$$c_f(x)=\frac{x\cdot f'(x)}{f(x)} = \frac{x\cdot\sin x}{1-\cos x} \approx \frac{x\cdot x}{x^2/2}=2.$$

Hence the unavoidable error is

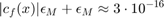
$$|c_f(x)|\epsilon_M + \epsilon_M \approx 3\cdot 10^{-16}$$

Therefore we should be able to achieve about 16 digits of accuracy in Matlab if we use a "good" algorithm.

format long g                                 % show results with 15 significant digits
x = 2e-6;
cf = x*sin(x)/(1-cos(x))
epsM = 1e-16;
unavoid_error = abs(cf)*epsM + epsM

cf =
          2.00004424441767
unavoid_error =
      3.00004424441767e-16

Algorithm 1: "Naive evaluation" of y = 1-cos(x)

We directly evaluate the formula 1-cos(x) in Matlab.

We compare yhat with the extra precision value ye and obtain a relative error of about 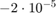$-2\cdot 10^{-5}$.

Since the actual error is much larger than the unavoidable error, algorithm 1 is numerically unstable.

x = 2e-6;  yhat = 1-cos(x)                     % naive evaluation result
xe = vpa('2*10^-6');  ye = vpa(1-cos(xe))      % extra precision result using vpa
relerr = double((yhat-ye)/ye)                  % relative error of yhat

yhat =
      1.99995575655976e-12
ye =
0.000000000001999999999999333333333333422131
relerr =
     -2.21217197881781e-05

Algorithm 2: Evaluate y = 2 sin(x/2)^2

We rewrite 1-cos(x) using the formulas cos(a+b)=cos(a)cos(b)-sin(a)sin(b) and 1-cos(t)^2=sin(t)^2:

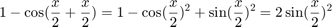
$$1-\cos(\frac{x}{2}+\frac{x}{2}) = 1 - \cos(\frac{x}{2})^2 + \sin(\frac{x}{2})^2=2\sin(\frac{x}{2})^2$$

We compare yhat with the extra precision value ye and obtain a relative error of about 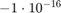$-1\cdot 10^{-16}$.

Since the actual error is not much larger than the unavoidable error, algorithm 2 is numerically stable.

x = 2e-6;  yhat = 2*sin(x/2)^2                 % using modified formula
relerr = double((yhat-ye)/ye)                  % relative error of yhat

yhat =
      1.99999999999933e-12
relerr =
      -1.0357477617381e-16


Published with MATLAB® R2016b