Solving a nonlinear least squares problem with the Gauss-Newton method and lsqnonlin

Contents

You need to download an m-file

Download the following m-file and put it in the same directory with your other m-files:

Given: three functions f1, f2, f3 of two variables x1,x2

Consider the functions

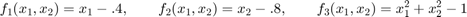
$$f_1(x_1,x_2)=x_1-.4,\qquad f_2(x_1,x_2)=x_2-.8,\qquad f_3(x_1,x_2)=x_1^2+x_2^2-1$$

Below are the zero contours of the three functions. We see that there is no point where all three functions are zero.

f = @(x) [ x(1)-.4; x(2)-.8 ; x(1)^2+x(2)^2-1 ];

zerocont2m(f,[.3 .7 .7 1]) % plot zero contours of the functions f_1, f_2, f_3
hold on

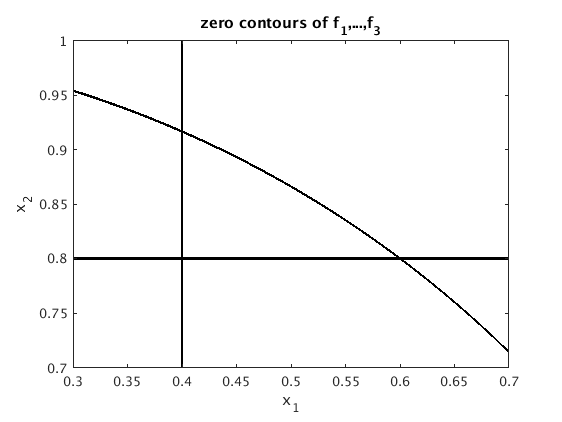
Least squares problem: minimize norm(f)

As we cannot achieve f(x)=[0;0;0] we want to find x such that norm(f(x)) is minimal. Below is a contour graph for norm(f(x)). We see that there is a point x where norm(f(x)) is minimal.

g = @(x1,x2) norm(f(x1*[1;0]+x2*[0;1]));  % we want to plot contour levels of g
ezcontour(g,[.3 .7 .7 1]); colorbar       % make contour plot (ignore warning)
title('contours for ||f(x)||_2')

Warning: Function failed to evaluate on array inputs; vectorizing the function
may speed up its evaluation and avoid the need to loop over array elements.

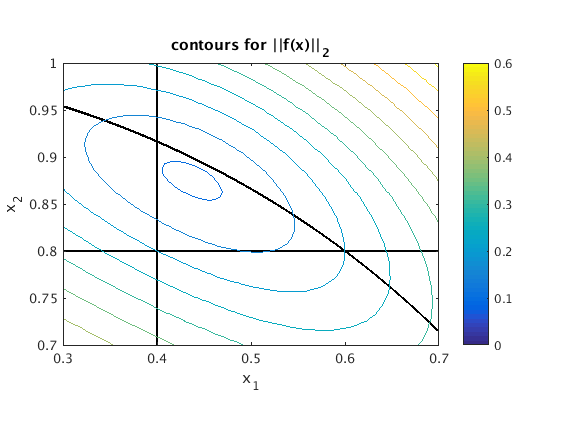
Gauss-Newton method

We first define the function fp(x) for the Jacobian matrix.

We start with the initial guess x=[0;0]. We see that the iteration converges to the point x = [.43752,.87504]. At this point norm(f(x)) has the minimal value .0942208.

fp = @(x) [ 1,0 ; 0,1 ; 2*x(1),2*x(2) ];  % define Jacobian fp(x)

format long g        % show all digits
x = [0;0];           % initial guess
while 1
  b = f(x);          % evaluate f
  A = fp(x);         % evaluate Jacobian
  d = -A\b;          % solve linear least squares problem norm(A*d+b)=min
  x = x + d
  if norm(d)<=1e-15  % stop iteration if norm(d)<=StepTolerance
    break
  end
end

fnorm = norm(f(x))   % norm of f(x) at minimum

plot(x(1),x(2),'k*'); hold off %    mark solution point with '*'
title('Solution of nonlinear least squares problem (*)')

x =
                       0.4
                       0.8
x =
         0.438095238095238
         0.876190476190476
x =
         0.437531075791456
         0.875062151582913
x =
         0.437520778200845
         0.875041556401689
x =
         0.437520595215861
         0.875041190431722
x =
         0.437520591965889
         0.875041183931778
x =
         0.437520591908167
         0.875041183816335
x =
         0.437520591907142
         0.875041183814284
x =
         0.437520591907124
         0.875041183814248
x =
         0.437520591907124
         0.875041183814247
fnorm =
        0.0942207695878639

Find errors for Gauss-Newton method

We have found a solution. We now run the iteration again to print the errors.

We see that the error improves by a factor of about .0178 with each iteration. Therefore we have convergence of order 1.

xs = x;              % xs is exact solution which we just found
x = [0;0];
enormold = NaN;
for i=1:10
  b = f(x);
  A = fp(x);
  d = -A\b;
  x = x + d;
  enorm = norm(x-xs);
  fprintf('enorm = %g, quotient = %g\n',enorm,enorm/enormold)
  enormold = enorm;
end

enorm = 0.0838986, quotient = NaN
enorm = 0.00128495, quotient = 0.0153155
enorm = 2.34427e-05, quotient = 0.0182441
enorm = 4.16565e-07, quotient = 0.0177695
enorm = 7.39856e-09, quotient = 0.0177609
enorm = 1.31404e-10, quotient = 0.0177607
enorm = 2.33383e-12, quotient = 0.0177608
enorm = 4.14583e-14, quotient = 0.0177641
enorm = 7.4476e-16, quotient = 0.0179641
enorm = 0, quotient = 0

Solving the nonlinear least squares problem with lsqnonlin

You can solve a nonlinear least squares problem |f(x)|=min using lsqnonlin. This has the following advantages:

f = @(x) [ x(1)-.4; x(2)-.8 ; x(1)^2+x(2)^2-1 ];  % define f
x0 = [0;0];                                       % initial guess
[xs,fnorm2] = lsqnonlin(f,x0)                     % find solution xs
fnorm = sqrt(fnorm2)

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the default value of the function tolerance.



xs =
         0.437520778647501
         0.875041556336608
fnorm2 =
       0.00887755342255288
fnorm =
        0.0942207695922342


Published with MATLAB® R2016b