Predator-Prey Problem
Contents
- Download this m-file
- System of differential equations
- Given initial conditions
- Definition of the function f
- Solve the ODE using the Euler method
- Solve the initial value problem using ode45
- Plot both y1(t) and y2(t) vs. t
- Plot y2 vs. y1 (phase plane plot)
- Solve ODE with higher accuracy, then make phase plane plot
Download this m-file
You first have to download the file
and put it in the same directory as your other m-files.
System of differential equations
Let y1 denote the number of rabbits (prey), let y2 denote the number of foxes (predator). The population growth is described by
- y1' = a1*y1
- y2' = a2*y2
Here the growth rate a1 for rabbits is positive for y2=0, but decreases with increasing y2; the growth rate a2 for foxes is negative for y1=0, but increases with increasing y1:
- a1 = 2 - .5*y2
- a2 = -1 + .5*y1
Hence we obtain the following system of ODEs
- y1' = (2-.5*y2)*y1
- y2' = (-1+.5*y1)*y2
Given initial conditions
The initial rabbit population is 6, the initial fox population is 2:
- y1(0) = 6
- y2(0) = 2
Definition of the function f
We have an ODE system y' = f(t,y) where y is a vector and the vector-valued function f is given by
f = @(t,y) [(2-.5*y(2))*y(1); (-1+.5*y(1))*y(2)];
Solve the ODE using the Euler method
Assume that at time t we have the vector y. Then we compute the slope vector s=f(t,y) and define the new y-vector by y = y + h*s.
We repeat this until we reach the final time T.
Note that the values of the Euler method are not very accurate for h=0.1.
y = [6;2]; t = 0; % given initial value h = .1; % step size for i=1:100 plot(t,y(1),'b.',t,y(2),'r.'); hold on % plot rabbits in blue, foxes in red s = f(t,y); % find slope vector y = y + h*s; % find new y-vector by using s t = t + h; end hold off legend('rabbits','foxes')
Solve the initial value problem using ode45
We want to find the functions y1(t) and y2(t) for t in [0,15].
In Matlab we use [ts,ys] = ode45(f,[t0,T],y0).
Here the input arguments are:
- f is the ODE function (can be defined by an @-function, or an m-file)
- t0 is the initial time
- T is the final time
- y0 is the initial y-vector at time t0.
This returns the arrays ts, ys:
- ts is the vector of time values (Matlab chooses h automatically at each step)
- ys is an array containing the values of y: row j contains the values of y1 (rabbits) and y2 (foxes) at the time ts(j) .
[ts,ys] gives a table with t in column 1, y1 (rabbits) in column 2, y2 (foxes) in column 3
[ts,ys] = ode45(f,[0,15],[6;2]);
[ts,ys] % table with values of t, y1, y2 in each row
ans =
0 6.0000 2.0000
0.0251 6.1486 2.1050
0.0502 6.2923 2.2196
0.0754 6.4296 2.3446
0.1005 6.5591 2.4808
0.2069 6.9969 3.1941
0.3133 7.1111 4.1963
0.4197 6.7843 5.4927
0.5262 6.0208 6.9653
0.6137 5.1515 8.1505
0.7013 4.1971 9.1635
0.7888 3.2782 9.9004
0.8763 2.4945 10.3010
0.9560 1.9375 10.3842
1.0357 1.5046 10.2662
1.1153 1.1755 9.9993
1.1950 0.9308 9.6282
1.3057 0.6956 9.0121
1.4163 0.5356 8.3476
1.5270 0.4187 7.6803
1.6377 0.3389 7.0278
1.7386 0.2951 6.4553
1.8395 0.2644 5.9184
1.9404 0.2430 5.4190
2.0413 0.2288 4.9575
2.1513 0.2199 4.4964
2.2612 0.2165 4.0768
2.3711 0.2179 3.6961
2.4811 0.2237 3.3517
2.6374 0.2395 2.9189
2.7937 0.2645 2.5460
2.9499 0.3002 2.2261
3.1062 0.3487 1.9527
3.3371 0.4508 1.6229
3.5679 0.6020 1.3683
3.7988 0.8248 1.1784
4.0296 1.1519 1.0472
4.1967 1.4775 0.9889
4.3638 1.9031 0.9627
4.5309 2.4532 0.9754
4.6980 3.1507 1.0418
4.8650 4.0046 1.1925
5.0321 5.0184 1.4699
5.1992 6.0903 1.9739
5.3663 6.9628 2.8857
5.4157 7.1245 3.2691
5.4652 7.2152 3.7155
5.5146 7.2210 4.2281
5.5640 7.1303 4.8061
5.6135 6.9355 5.4442
5.6629 6.6364 6.1291
5.7124 6.2414 6.8408
5.7618 5.7669 7.5537
5.8406 4.9091 8.6141
5.9193 4.0192 9.4919
5.9981 3.1857 10.1190
6.0769 2.4763 10.4609
6.1518 1.9408 10.5379
6.2268 1.5209 10.4293
6.3017 1.1983 10.1813
6.3767 0.9553 9.8339
6.4820 0.7155 9.2451
6.5873 0.5508 8.6030
6.6926 0.4307 7.9520
6.7980 0.3479 7.3110
6.8961 0.3000 6.7334
6.9942 0.2660 6.1891
7.0924 0.2419 5.6807
7.1905 0.2252 5.2090
7.2970 0.2139 4.7376
7.4035 0.2081 4.3069
7.5101 0.2069 3.9147
7.6166 0.2098 3.5584
7.7638 0.2204 3.1202
7.9110 0.2385 2.7388
8.0582 0.2650 2.4080
8.2054 0.3012 2.1220
8.4423 0.3854 1.7435
8.6792 0.5125 1.4502
8.9161 0.7027 1.2285
9.1530 0.9859 1.0699
9.3284 1.2790 0.9914
9.5038 1.6692 0.9458
9.6791 2.1839 0.9381
9.8545 2.8522 0.9805
9.9937 3.5072 1.0657
10.1329 4.2840 1.2148
10.2721 5.1624 1.4650
10.4112 6.0746 1.8844
10.5057 6.6519 2.3133
10.6002 7.1044 2.9173
10.6947 7.3348 3.7426
10.7892 7.2474 4.8119
10.8574 6.9411 5.7304
10.9256 6.4349 6.7267
10.9938 5.7649 7.7362
11.0620 4.9923 8.6823
11.1302 4.1965 9.4829
11.1984 3.4424 10.0883
11.2666 2.7736 10.4783
11.3348 2.2138 10.6557
11.4057 1.7487 10.6446
11.4766 1.3848 10.4801
11.5475 1.1036 10.2026
11.6184 0.8899 9.8454
11.7113 0.6877 9.3046
11.8041 0.5445 8.7247
11.8970 0.4397 8.1366
11.9899 0.3646 7.5568
12.0920 0.3089 6.9412
12.1941 0.2699 6.3603
12.2962 0.2425 5.8184
12.3983 0.2237 5.3165
12.5019 0.2116 4.8476
12.6055 0.2048 4.4178
12.7090 0.2025 4.0252
12.8126 0.2041 3.6675
12.9561 0.2125 3.2250
13.0996 0.2278 2.8383
13.2430 0.2507 2.5014
13.3865 0.2823 2.2088
13.6312 0.3609 1.7983
13.8759 0.4819 1.4818
14.1207 0.6659 1.2432
14.3654 0.9441 1.0725
14.5240 1.1946 0.9959
14.6827 1.5195 0.9458
14.8413 1.9384 0.9247
15.0000 2.4731 0.9392
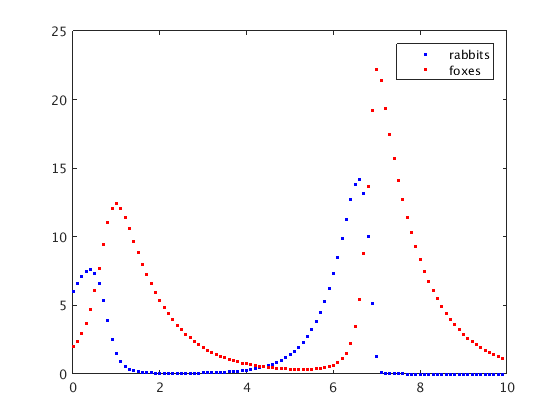
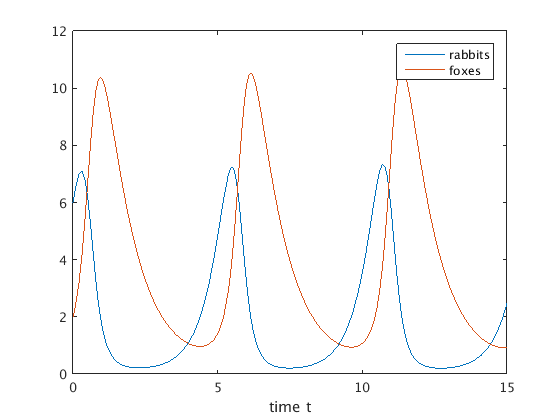
Plot both y1(t) and y2(t) vs. t
We can plot the rabbit population vs. t using plot(ts,ys(:,1)) since ys(:,1) gives the first column of the array ys with the rabbit values.
We can plot both rabbits and foxes vs. t using plot(ts,ys). Matlab now plots the first column of ys (rabbits) in blue, and the second column of ys (foxes) in red.
It appears that the functions y1(t), y2(t) are periodic with a period of about 5.
plot(ts,ys) % plot rabbit and fox population vs. t legend('rabbits','foxes'); xlabel('time t')
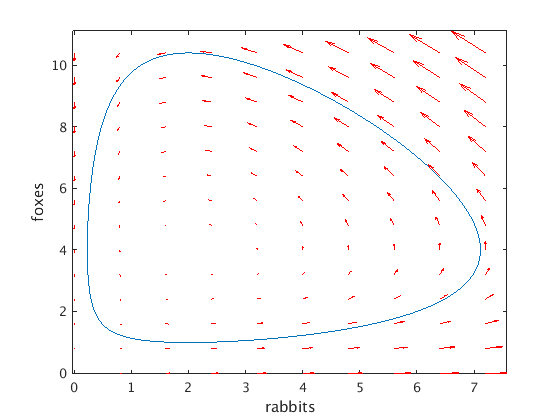
Plot y2 vs. y1 (phase plane plot)
We can also consider the solution (y1(t),y2(t)) as tracing a curve in the (y1,y2) plane ("phase plane"). We can plot this curve with plot(ys(:,1),ys(:,2)).
The phase plane plot should be a closed curve since the solution is periodic.
The vector field given by f shows the velocity vectors with which the point (y1(t),y2(t)) moves along the trajectory. We see that the point moves along the closed curve counterclockwise as t increases.
Note that we do not quite get a closed curve: after one period we arrive at a slightly different point. This is due to the error of the numerical method in ode45.
plot(ys(:,1),ys(:,2)); hold on % plot solution in phase plane xlabel('rabbits'); ylabel('foxes') vectfield(f,0:.8:7.5,0:.8:10.5); hold off % plot vector field
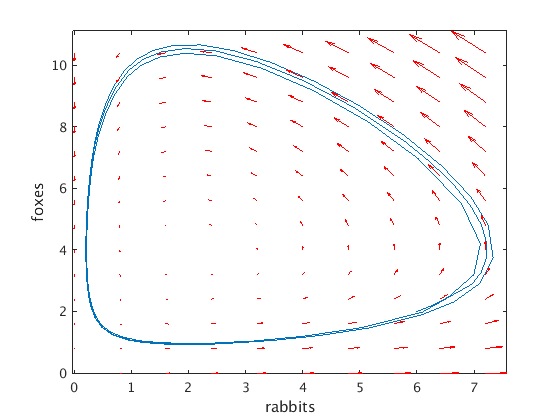
Solve ODE with higher accuracy, then make phase plane plot
We can define additional options using odeset. Here we specify a tolerance of 1e-10 for both the relative error ('RelTol') and the absolute error ('AbsTol').
Now the errors are much smaller, and we obtain a closed curve (at least for the visual accuracy of the plot).
opt = odeset('RelTol',1e-10,'AbsTol',1e-10); % use smaller tolerances [ts,ys] = ode45(f,[0,15],[6;2],opt); % use opt defined by odeset plot(ys(:,1),ys(:,2)); hold on % plot solution in phase plane xlabel('rabbits'); ylabel('foxes') vectfield(f,0:.8:7.5,0:.8:10.5); hold off % plot vector field