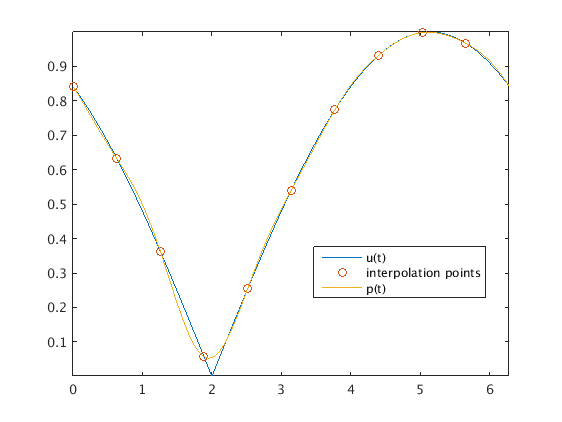
Interpolate a periodic function by trigonometric polynomial, even number of nodes

Contents

Plot function and interpolation points

We want to approximate the 2 pi periodic function u(t) = abs(sin(t/2-1)) using 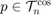$p\in {\cal T}_n^{\cos}$ with n=5. This space has dimension m=10, so we use 10 equidistant data points j*2*pi/m, j=0,...,m-1.

u = @(t) abs(sin(t/2-1));
m = 10;                    % even number of data points
t = (0:m-1)'*2*pi/m;       % interpolation points

U = u(t);                  % data used for interpolation

mp = 1000;                 % for plotting use finer mesh of mp=1000 equidistant points
tp = (0:mp-1)'*2*pi/mp;
plot(tp,u(tp),t,U,'o'); hold on  % plot function at points tp, points used for interpolation

Apply the Discrete Fourier Transform

We want to find the interpolating function

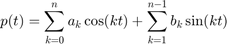
$$p(t) = \sum_{k=0}^n a_k \cos(kt) + \sum_{k=1}^{n-1} b_k \sin(kt)$$

We use the FFT to obtain the coefficient vectors $[a_0,\ldots,a_n]$ and $[b_1,\ldots,b_{n-1}]$.

[a,b] = cossin_transform(U);  % coefficients of interpolating function

Extend the coefficient vectors with zeros, apply the inverse transform

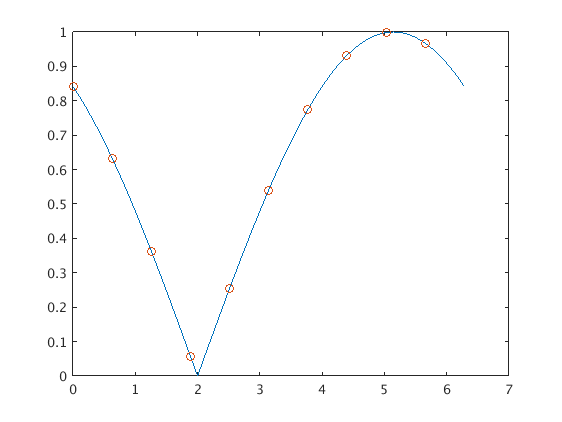
We want to evaluate the interpolating function on a finer mesh with mp points. We extend the a and b vectors with zeros for higher frequencies.

These padded coefficient vectors ap and bp still represent the same interpolating function, but now the inverse transform yields values on a finer mesh.

K = (mp-m)/2;
ap = [a;zeros(K,1)];       % extend a and b vector with K zeros
bp = [b;zeros(K,1)];

Up = inv_cossin_transform(ap,bp);  % this gives now function values on fine grid with 1000 points tp

plot(tp,Up); hold off; axis tight
legend('u(t)', 'interpolation points', 'p(t)','Location','best')
hold off


Published with MATLAB® R2015a