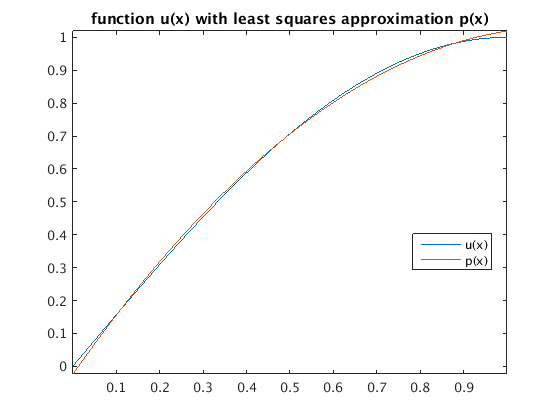
Example for least squares approximation

Contents

Computing the coefficient vector

We want to approximate the function 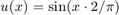$u(x) = \sin(x\cdot2/\pi)$ on the interval [0,1], using the functions $1,x,\ldots,x^{n-1}$.

We use the normal equations to find the least squares approximation p which minimizes

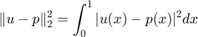
$$\|u-p\|_2^2 = \int_0^1 |u(x)-p(x)|^2 dx$$

n = 3;                       % find approximation with polynomial of degree <=n-1

M = findmatrix(n);           % see separate m-files findmatrix.m, findrhsvector.m
b = findrhsvector(n);
c = M\b                      % find c by solving the normal equations

c =
       -0.0243249469630999
          1.87827195473064
        -0.834573774103911

Plot function p(x) and find error 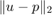$\|u-p\|_2$

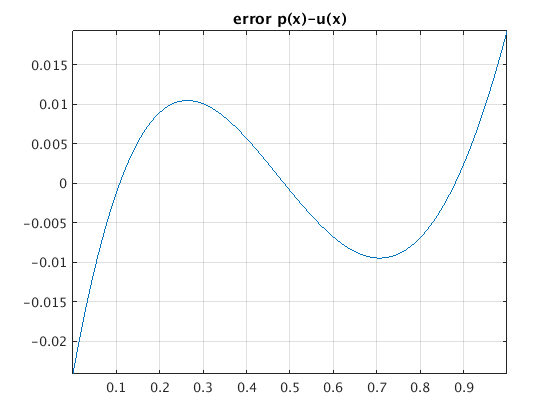
N = 1000;                    % find L2-error approximatively using midpoint rule with N subintervals
x = ((1:N)'-.5)/N;           % midpoints of subintervals
ux = sin(pi/2*x);            % values of u(x)

px = ones(N,1)*c(n);         % evaluate p(x) using nested multiplication
for j=n-1:-1:1
  px = px.*x + c(j);
end

figure(1)
plot(x,ux,x,px);
axis tight; legend('u(x)','p(x)','Location','best')
title('function u(x) with least squares approximation p(x)')

ex = px - ux;
figure(2)
plot(x,ex)                   % plot error e(x) = p(x)-u(x)
axis tight; grid on; title('error p(x)-u(x)')

L2error = sqrt( sum(abs(ex).^2)/N )   % approximate L2-error ||u-p|| using midpoint rule

L2error =
       0.00838180452644634


Published with MATLAB® R2015a