The Poisson problem -Delta u = f on a square
Contents
The domain is the square [0,1]^2. For the function f(x)=1 we want to find the solution u(x1,x2) of the equation
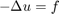
with the boundary condition u=0 on the boundary of the square.
We want to find the displacement in the center
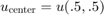
and plot the graph of u(x).
We use a uniform mesh with meshsize h=1/N.
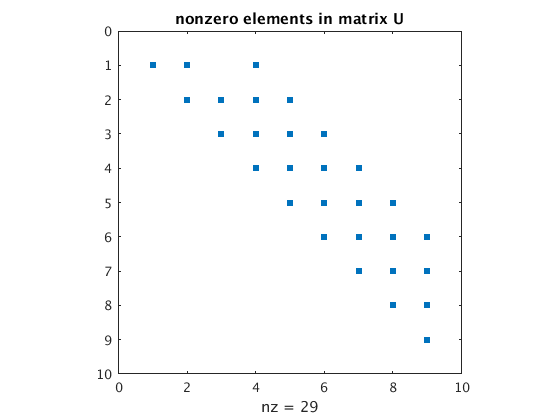
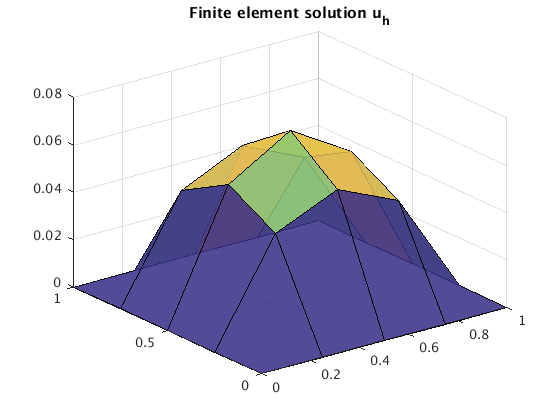
N=4
N = 4; h = 1/N; n = (N-1)^2 % n is number of unknowns A = laplacian2(N); % generate A as sparse matrix b = ones(n,1)*h^2; % right hand side vector % Gaussian elimination with row pivoting: [L,U,p] = lu(A,'vector'); % Find LU-decomposition y = L\b(p); % use forward substitution to find y u = U\y; % use back substitution to find u ucenter = u((n+1)/2) % displacement in center full(A) % show full matrix figure(1); spy(U) % show sparsity structure of matrix U title('nonzero elements in matrix U') x=(0:N)/N; v=zeros(N+1,N+1); v(2:N,2:N)=reshape(u,N-1,N-1); figure(2); surf(x,x,v'); alpha(.85) title('Finite element solution u_h')
n =
9
ucenter =
0.0703
ans =
4 -1 0 -1 0 0 0 0 0
-1 4 -1 0 -1 0 0 0 0
0 -1 4 0 0 -1 0 0 0
-1 0 0 4 -1 0 -1 0 0
0 -1 0 -1 4 -1 0 -1 0
0 0 -1 0 -1 4 0 0 -1
0 0 0 -1 0 0 4 -1 0
0 0 0 0 -1 0 -1 4 -1
0 0 0 0 0 -1 0 -1 4
N=20, no reordering
The matrix A is a band matrix with bandwidth b = sqrt(n). Since most of the band is filled in we expect about n*sqrt(n)=6859 nonzero elements in U.
Actually the matrix U has 6877 nonzero elements (slightly less, because of the empty triangle at the top).
N = 20; h = 1/N; n = (N-1)^2 % n is number of unknowns A = laplacian2(N); % generate A as sparse matrix b = ones(n,1)*h^2; % right hand side vector % Gaussian elimination with row pivoting: [L,U,p] = lu(A,'vector'); % Find LU-decomposition y = L\b(p); % use forward substitution to find y u = U\y; % use back substitution to find u ucenter = u((n+1)/2) % displacement in center figure(1); spy(U) % show sparsity structure of matrix U title('nonzero elements in matrix U') x=(0:N)/N; v=zeros(N+1,N+1); v(2:N,2:N)=reshape(u,N-1,N-1); figure(2); surf(x,x,v'); alpha(.85) title('Finite element solution u_h')
n =
361
ucenter =
0.0735
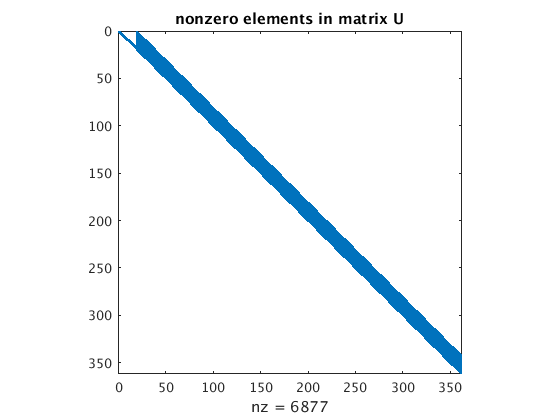
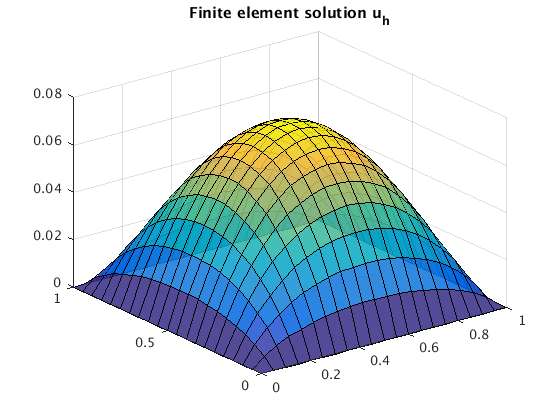
N=20, with reordering
Now Matlab reorders the unknows in order to minimize the "fill-in".
We see that Matlab finds a permutation q for the unknowns such that the matrix U has 3246 nonzero elements (instead of 6877 before).
N = 20; h = 1/N; n = (N-1)^2 % n is number of unknowns A = laplacian2(N); % generate A as sparse matrix b = ones(n,1)*h^2; % right hand side vector % Gaussian elimination with row and column pivoting % choose column pivoting to minimize fill-in [L,U,p,q] = lu(A,'vector'); % Find LU-decomposition y = L\b(p); % use forward substitution to find y u = U\y; u(q)=u; % use back substitution to find u, undo permutation q ucenter = u((n+1)/2) % displacement in center figure(1); spy(U) % show sparsity structure of matrix U title('nonzero elements in matrix U with reordering')
n =
361
ucenter =
0.0735
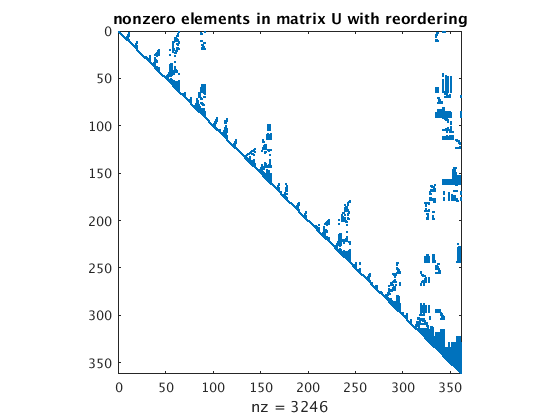
N=1000, with reordering
The backslash command u=A\b in Matlab tries to find the best possible algorithm for solving a linear system. It considers using algorithms for tridiagonal matrices, band matrices, Cholesky decomposition (if A is symmetric positive definite), and different reordering strategies.
With the command spparms('spumoni',2) we can see what algorithms Matlab is considering.
We have a matrix of size n by n where n is almost 10^6. The time to solve this linear system is under 5 seconds. The number of operations ("flops") is about 2e10, the number of nonzero elements in the matrix L is about 4.4e7.
Note that without reordering we would have about n*sqrt(n) nonzero elements in the matrix L, this is about 10^6*10^3=10^9.
N = 1000; h = 1/N; n = (N-1)^2 % n is number of unknowns A = laplacian2(N); % generate A as sparse matrix b = ones(n,1)*h^2; % right hand side vector % Gaussian elimination with row and column pivoting spparms('spumoni',2) % show information about algorithms used by \ disp('SHOW INFORMATION ABOUT ALGORITHMS USED BY "\":') tic; u = A\b; toc disp('(time to solve n by n linear system)') ucenter = u((n+1)/2) % displacement in center spparms('spumoni',0) % stop displaying extra information for \
n =
998001
SHOW INFORMATION ABOUT ALGORITHMS USED BY "\":
sp\: bandwidth = 999+1+999.
sp\: is A diagonal? no.
sp\: is band density (0.0025005) > bandden (0.5) to try banded solver? no.
sp\: is A triangular? no.
sp\: is A morally triangular? no.
sp\: is A a candidate for Cholesky (symmetric, real positive diagonal)? yes.
sp\: is CHOLMOD's symbolic Cholesky factorization (with automatic reordering) successful? yes.
sp\: is CHOLMOD's numeric Cholesky factorization successful? yes.
sp\: is CHOLMOD's triangular solve successful? yes.
CHOLMOD version 1.7.0, Sept 20, 2008: : status: OK
Architecture: Linux
sizeof(int): 4
sizeof(UF_long): 8
sizeof(void *): 8
sizeof(double): 8
sizeof(Int): 8 (CHOLMOD's basic integer)
sizeof(BLAS_INT): 8 (integer used in the BLAS)
Results from most recent analysis:
Cholesky flop count: 1.9867e+10
Nonzeros in L: 4.4369e+07
memory blocks in use: 13
memory in use (MB): 624.1
peak memory usage (MB): 712.0
maxrank: update/downdate rank: 8
supernodal control: 1 40 (supernodal if flops/lnz >= 40)
nmethods=0: default strategy: Try user permutation if given. Try AMD.
Select best ordering tried.
method 0: user permutation (if given)
method 1: AMD (or COLAMD if factorizing AA')
prune_dense: for pruning dense nodes: 10
a dense node has degree >= max(16,(10)*sqrt(n))
flop count: 1.9867e+10
nnz(L): 4.4369e+07
final_asis: TRUE, leave as is
dbound: LDL' diagonal threshold: 0
Entries with abs. value less than dbound are replaced with +/- dbound.
grow0: memory reallocation: 1.2
grow1: memory reallocation: 1.2
grow2: memory reallocation: 5
nrelax, zrelax: supernodal amalgamation rule:
s = # columns in two adjacent supernodes
z = % of zeros in new supernode if they are merged.
Two supernodes are merged if (s <= 4) or (no new zero entries) or
(s <= 16 and z < 80%) or (s <= 48 and z < 10%) or (z < 5%)
OK
Elapsed time is 4.327856 seconds.
(time to solve n by n linear system)
ucenter =
0.0737