0
Hyperbolic and parabolic equations are the two most important categories of
time-dependent problems whose evolution process is well-posed. Thus, consider
the initial value problem
We assume that a large enough class of admissible initial data
there exists a unique solution, u(x,t). This defines a solution operator,
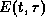which describes the evolution of the problem
Hoping to compute such solutions, we need that the solutions will depend
continuously in their initial data, i.e.,
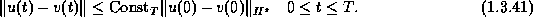
In view of linearity, this amounts to having the a priori estimate
(boundedness)
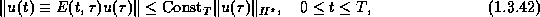
which includes the hyperbolic and parabolic cases.
: (Hadamard) By Cauchy-Kowalewski, the system
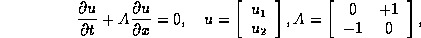
has a unique solution for arbitrary analytic data, at least for
sufficiently small time. Yet, with initial data
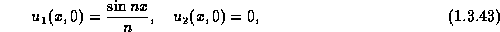
we obtain the solution
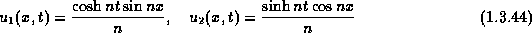
which tends to infinity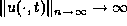 
, while the initial data
tend to zero. Thus, the Laplace
equation,
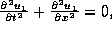is not well-posed as an initial-value problem.
Finally, we note that a well-posed problem is stable against perturbations of inhomogeneous data in view of the following
. The solution of the inhomogeneous problem
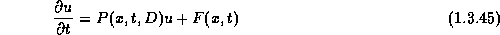
is given by
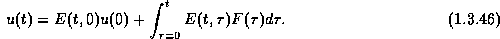
Indeed, a straightforward substitution yields
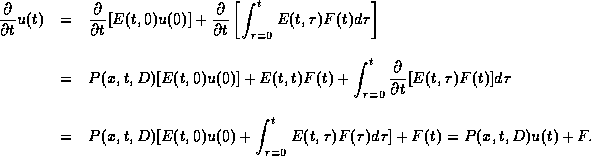
This implies the a priori stability estimate
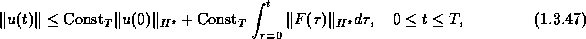
as asserted.