0
Consider the first order Sturm-Liouville (SL) problem
augmented with periodic boundary conditions
It has an infinite sequence of eigenvalues, 
, with the
corresponding eigenfunctions 
. Thus, 
are the eigenpairs of the
differentiation operator 
in 
, and
they form a in this space --
completeness in the sense described below.
Let the space
be endowed with the usual Euclidean inner product
Note that are orthogonal with respect
to this inner product,
for
Let 
be associated with its spectral
representation in this system, i.e., the Fourier expansion
or equivalently,
The truncated Fourier expansion
denotes the spectral-Fourier projection of w(x) into 
-the space
of trigonometric polynomials of degree 
:
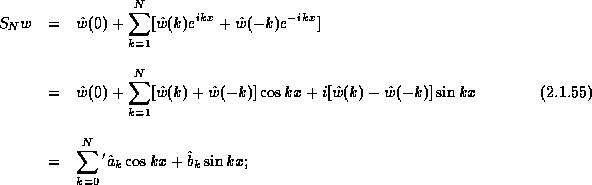
here 
and 
are the usual Fourier coefficients
given by
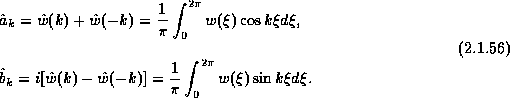
Since 
is orthogonal to the -space:
it follows that for any 
we have
(see Figure 2.1 )
Figure 2.1: Least-squares approximation
Hence, solves the least-squares problem
i.e., is the best least-squares approximation to w. Moreover,
(app_fourier.11) with yields
and by letting we arrive at
: An immediate consequence of (app_fourier.14) is the
Riemann-Lebesgue lemma, asserting that
The system is in the sense
that for any we have
which in view of (app_fourier.13), is the same as
Thus completeness guarantee that the spectral projections 'fill in'
the relevant space.
The last equality establishes the 
convergence of the
spectral-Fourier projection, , to w(x), whose difference can be
(upper-)bounded by the following
:
We observe that the RHS tends to zero as a tail of a converging sequence,
i.e.,
The last equality tells us that the convergence rate depends on how fast the
Fourier coefficients, , decay to zero, and we shall quantify this
in a more precise way below.
. What about pointwise convergence?
The -convergence stated in (app_fourier.17)
yields pointwise a.e. convergence for
subsequences; one can show that in fact
The ultimate result in this direction states that ,
(no subsequences)
for all
, though a.e. convergence may fail if is
only -integrable.
The question of pointwise a.e. convergence is an extremely intricate issue
for arbitrary -functions.
Yet, if we agree to assume sufficient smoothness, we find the
convergence of spectral-Fourier projection to be very rapid,
both in the
and the pointwise sense. To this we proceed as follows.