Hyperbolic systems with variable coefficients

We want to extend our previous analysis to linear systems of the form
 
This is the motivation for the definition of hyperbolicity (1.1.18) in the context of constant coefficient problems: freeze the coefficients and assume the hyperbolicity of the constant coefficient problem(s), , uniformly for each ; then - in contrast to the notion of weak hyperbolicity, the variable coefficients problem is also hyperbolic. This result is based on the invariance of the notion of hyperbolicity under low-order perturbations.

As before the study of the variable coefficients problem can be carried out by one of two ways:

• by the Fourier method - one characterize the hyperbolicity of (hyper.25) in terms of the algebraic properties of the pseudodifferential symbol, ;
• alternatively, we can also work directly in physical space with the energy method. For example, if we assume that P(x,t,D) is semi-bounded, i.e., if
   
  then we have hyperbolicity (1.1.18).

: The symmetric hyperbolic case : we can rewrite such symmetric problems in the equivalent form

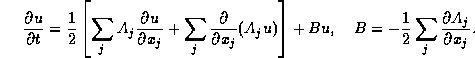
In this case the symmetry of the 's implies that is skew-adjoint, i.e., integration by parts gives

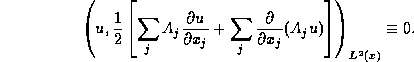
Therefore we have

and hence the semi-boundedness requirement (hyper.26) holds with . Consequently, if are symmetric (or at least symmetrizable) then the system (1.1.17) is hyperbolic.