Demo on Differential Equations, Math 141, Fall 2012

Contents

Direction Fields

Say we want to study an equation like

$$y' = xy + 2.$$

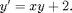
We can start by drawing a "direction field", showing the slopes $dy/dx$ at various points.

[xx, yy] = meshgrid(-2:.5:2, -2:.5:2);
quiver(xx, yy, ones(size(xx)), xx.*yy + 2)
title 'direction field for y'' = xy + 2'

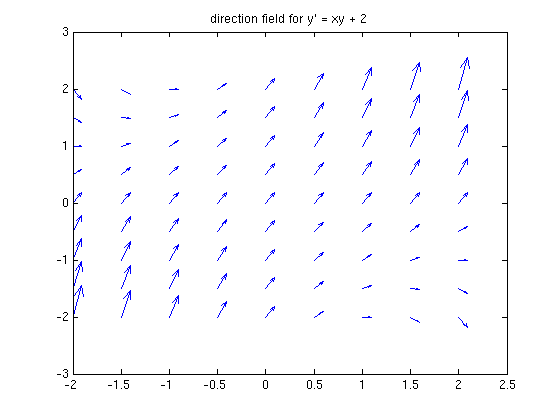
From the picture, we can visualize what the solutions look like. We can also solve for them analytically:

syms x c
sol = dsolve('Dy = x*y + 2', 'y(0) = c', 'x')

 
sol =
 
c*exp(x^2/2) + 2^(1/2)*pi^(1/2)*exp(x^2/2)*erf((2^(1/2)*x)/2)

Solution Curves

The answer is in terms of a constant of integration c. Let's plot the solutions for different values of c on the same axes.

hold on
for j = -2:.5:2
    ezplot(subs(sol, c, j), [-2, 2]), axis([-2, 2, -2 2])
end
hold off
title 'direction field and solution curves for y'' = xy + 2'

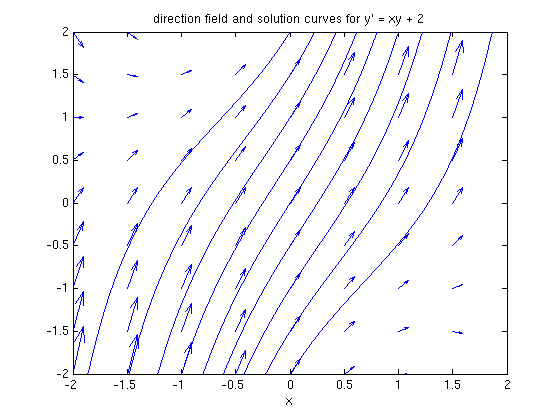
Nonlinear Equations

The equation above is linear, which implies that there is a closed-form solution. When an equation is non-linear, as in the following example

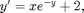
$$y' = xe^{-y} + 2,$$

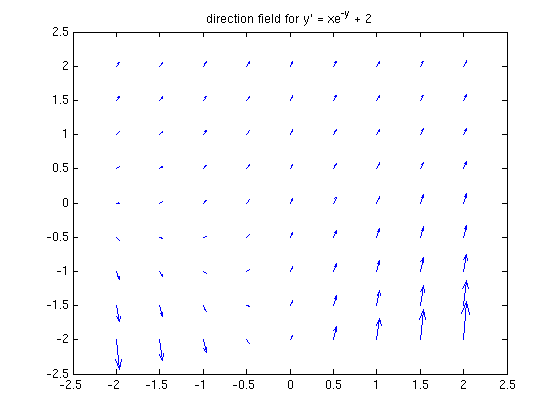
it may or may not be possible to solve explicitly, though one can always solve numerically given an initial condition. Here is the "direction field", showing the slopes 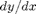$dy/dx$ at various points.

quiver(xx, yy, ones(size(xx)), xx.*exp(-yy) + 2)
title 'direction field for y'' = xe^{-y} + 2'
sol1 = dsolve('Dy = x*exp(-y) + 2', 'y(0) = c', 'x')

 
sol1 =
 
- log(-1/(2*x - 4*exp(2*x)*(exp(c) + 1/4) + 1)) - 2*log(2)

Let's superimpose some solution curves.

hold on
for j = -2:.5:2
    ezplot(subs(sol1, c, j), [-2, 2]), axis([-2, 2, -2 2])
end
hold off
title 'direction field and solution curves for y'' = xe^{-y} + 2'

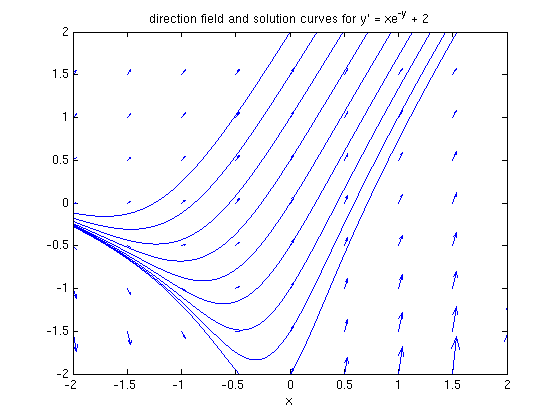
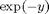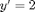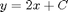In this case the solution curves at the top of the picture all look like straight lines. This makes sense, since for y large, $\exp(-y)$ is almost 0, and so the equation looks like $y' = 2$, which has solution curves of the form $y = 2x + C$.


Published with MATLAB® R2012b