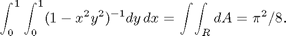Change of Variables in Multiple Integrals
copyright © 2009 by Jonathan Rosenberg based on an earlier M-book, copyright © 2000 by Paul Green and Jonathan Rosenberg
Contents
Changing Variables in Double Integrals
In this lesson, we will learn to evaluate integrals using a suitable change of variables. For our first example, we will consider
where R is the region in the first quadrant bounded by the circles x^2 + y^2 = 1 and x^2 + y^2 = 4, and the parabolae y = x^2 and y = 3*x^2. Let's begin by drawing a picture of the region R.
syms x y ezplot(x^2+y^2-1, [0, 2, 0, 2]); hold on; ezplot(x^2+y^2-4, [0, 2, 0, 2]); ezplot(x^2,[0,2]); ezplot(3*x^2,[0,2]); axis equal; axis([0,2,0,2]); title('region bounded by two circles and two parabolae'); hold off
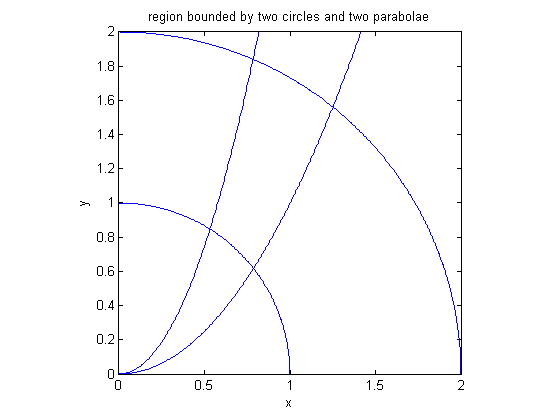
While the region R is clearly visible in the problem, we also see why it's so difficult to do the integration in rectangular coordinates: regardless of what order of integration we choose, we will have to split the region into pieces, and the limits of integration will look quite different in each. This suggests that a much better approach is to change variables. We convert the region of integration to a rectangle in the uv-plane, by setting u = x^2 + y^2 and v = y/x^2. (This is not the only reasonable choice of a new coordinate system, but it's one that is easily suggested by the equations of the bounding curves.) In order to formulate the integral, we must first solve for x and y in terms of u and v.
syms u v [xfun,yfun]=solve(x^2+y^2-u, y-x^2*v,x,y); [xfun,yfun]
ans = [ (((4*u*v^2 + 1)^(1/2) - 1)/(2*v^2))^(1/2), ((4*u*v^2 + 1)^(1/2) - 1)/(2*v)] [ (-((4*u*v^2 + 1)^(1/2) + 1)/(2*v^2))^(1/2), -((4*u*v^2 + 1)^(1/2) + 1)/(2*v)] [ -(-1/2/v^2*((4*u*v^2 + 1)^(1/2) + 1))^(1/2), -((4*u*v^2 + 1)^(1/2) + 1)/(2*v)] [ -(1/2/v^2*((4*u*v^2 + 1)^(1/2) - 1))^(1/2), ((4*u*v^2 + 1)^(1/2) - 1)/(2*v)]
We are given our choice of four solutions. To choose the correct one, we observe that since u is going to run from 1 to 4, and v from 1 to 3, we should obtain values of x and y in the first quadrant when, for instance, u = v = 2.
subs([xfun,yfun],[u,v],[2,2])
ans = 0.7701 1.1861 0.0000 + 0.9182i -1.6861 -0.0000 - 0.9182i -1.6861 -0.7701 1.1861
Only the first solution satisfies our requirement. Accordingly, we set
newvar=[xfun(1),yfun(1)]
newvar = [ (((4*u*v^2 + 1)^(1/2) - 1)/(2*v^2))^(1/2), ((4*u*v^2 + 1)^(1/2) - 1)/(2*v)]
Next, we must compute the determinant that is called the Jacobian in your text. Unfortunately, there is a clash of notation between MATLAB and Ellis and Gulick. The jacobian function in MATLAB returns the actual matrix of partial derivatives. The integrating factor we want is the absolute value of the determinant of that matrix. Since MATLAB sometimes has trouble simplifying expressions involving absolute values, we suggest that you first compute just the determinant, and then change the sign if necessary (if the determinant turns out to be negative). To figure out whether the factor goes in the numerator or denominator, it's convenient to remember what happens with functions of one variable, where dx gets transformed to
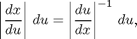
Similarly, in converting from dx dy to du dv, we can either multiply by the absolute value of the determinant of the matrix of partials of x and y with respect to u and v, or else by the reciprocal of the absolute value of the determinant of the matrix of partials of u and v with respect to x and y.
intfactor=det(jacobian(newvar))
intfactor = ((4*u*v^2 + 1)^(1/2) - 1)/(4*v^2*(4*u*v^2 + 1)^(1/2)*(((4*u*v^2 + 1)^(1/2) - 1)/(2*v^2))^(1/2))
%As a test of the sign:
subs(intfactor,[u,v],[2,2])
ans =
0.0670
Since this is positive, we don't need to insert a minus sign. We can now proceed to evaluate the integral, in this case either symbolically or numerically. We shall do both and compare the answers.
symbans=symint2(newvar(1)*newvar(2)*intfactor,u,1,4,v,1,3) numans=numint2(newvar(1)*newvar(2)*intfactor,u,1,4,v,1,3) double(symbans-numans)
Warning: Explicit integral could not be found.
symbans =
(17*17^(1/2))/48 - (5*5^(1/2))/48 + (37*37^(1/2))/3888 - (145*145^(1/2))/3888 - 1/3
numans =
0.5028
ans =
2.0071e-008
We see that the answers agree to five decimal places.
There is still one more way to do this problem; we could have changed into polar coordinates. This changes the equations of the circles x^2 + y^2 = 1 and x^2 + y^2 = 4 to the much simpler forms r = 1, r = 2. Thus we should be able to do the integration in polar coordinates with the r-integral on the outside. We still have to solve for theta in the equations of the parabolae.
syms r theta firstparab = solve(subs(y-x^2,[x,y],[r*cos(theta),r*sin(theta)]),theta)
firstparab =
pi + asin(((4*r^2 + 1)^(1/2) + 1)/(2*r))
-asin(1/2/r*((4*r^2 + 1)^(1/2) + 1))
pi - asin(1/2/r*((4*r^2 + 1)^(1/2) - 1))
asin(((4*r^2 + 1)^(1/2) - 1)/(2*r))
Again, we can see which solution is correct by evaluating at, say, r=1.5.
double(subs(firstparab,r,1.5))
ans = 4.7124 - 0.8541i -1.5708 + 0.8541i 2.3367 0.8049
Since we want to be in the first quadrant (where theta runs from 0 to pi/2=1.57), the last solution is the correct one. So we rewrite
firstparab=simplify(firstparab(4))
firstparab = asin(((4*r^2 + 1)^(1/2) - 1)/(2*r))
Now we do the same with the second parabola.
secparab = solve(subs(y-3*x^2,[x,y], ...
[r*cos(theta),r*sin(theta)]),theta)
double(subs(secparab,r,1.5))
secparab =
pi + asin(((36*r^2 + 1)^(1/2) + 1)/(6*r))
-asin(1/6/r*((36*r^2 + 1)^(1/2) + 1))
pi - asin(1/6/r*((36*r^2 + 1)^(1/2) - 1))
asin(((36*r^2 + 1)^(1/2) - 1)/(6*r))
ans =
4.7124 - 0.4797i
-1.5708 + 0.4797i
2.0331
1.1085
Again we want the last solution:
secparab = simplify(secparab(4))
secparab = asin(((36*r^2 + 1)^(1/2) - 1)/(6*r))
Also we see that the first parabola gives the lower limit of integration. Since there is an extra factor of r when we integrate in polar coordinates, the integral becomes:
symint2(r*cos(theta)*r*sin(theta)*r,...
theta,firstparab,secparab,r,1,2)
double(ans)
ans =
(17*17^(1/2))/48 - (5*5^(1/2))/48 + (37*37^(1/2))/3888 - (145*145^(1/2))/3888 - 1/3
ans =
0.5028
This is the same answer we obtained before in the u-v coordinate system. As a check, the difference between the two solutions is:
double(ans - symbans)
ans = 3.3544e-017
Problem 1
Use a suitable change of variables to evaluate the integral
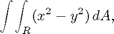
where R is the region in the first quadrant bounded by the ellipses x^2 + 3*y^2 = 3 and x^2 + 3*y^2 = 9, and the hyperbolae x^2 - 2*y^2 = 1 and x^2 - 2*y^2 = 4.
Changing Variables in Triple Integrals
We will now illustrate a three dimensional change of variables by integrating over a portion of the region inside a hyperboloid of one sheet. We will compute the volume of the region inside the hyperboloid for z between -4 and 4. We begin by recalling that the hyperboloid itself can be parametrized by
syms s t z hyp=[cosh(s)*cos(t)*sqrt(6),cosh(s)*sin(t)*sqrt(3),sinh(s)*sqrt(2)]
hyp = [ 6^(1/2)*cosh(s)*cos(t), 3^(1/2)*cosh(s)*sin(t), 2^(1/2)*sinh(s)]
Just as a check we've done this right:
simplify(subs(x^2+2*y^2-3*z^2,[x,y,z],hyp))
ans = 6
Next, to parametrize the solid region inside the hyperboloid, we introduce a factor, which we call r, into the x and y coordinates. (Caution: this is not the same as the r in cylindrical coordinates, though it plays a similar role.) If we let r run from 0 to 1, this parametrizes the solid region.
syms r
hypsol = [r,r,1].*hyp
hypsol = [ 6^(1/2)*r*cosh(s)*cos(t), 3^(1/2)*r*cosh(s)*sin(t), 2^(1/2)*sinh(s)]
Note the convenient use here of MATLAB's vector routines: .* computes the element-by-element product of two vectors. Now we have to compute the integrating factor, determine the limits of integration, and evaluate the volume of the solid.
intfac=simplify(det(jacobian(hypsol)))
intfac = (-6)*r*cosh(s)^3
Since this came out negative, we will have to cancel out the minus sign. The limits for r, as we have already observed, are 0 and 1. The limits for t are 0 and 2*pi, and since the limits for z are 4 and -4, the limits for s are:
slim1=solve(hyp(3)+4); slim2=solve(hyp(3)-4); [slim1,slim2] hypvol=int(int(int(-intfac,s,slim1,slim2),t,0,2*pi),r,0,1)
ans = [ -asinh(2*2^(1/2)), asinh(2*2^(1/2))] hypvol = 88*pi*2^(1/2)
The numerical value is:
double(hypvol)
ans = 390.9737
If instead of the volume, which is equivalent to the integral of the function 1, we wished to compute the integral of a function such as z^2 over the same solid region, we must express it in terms of the new variables and include it as a factor in the integrand.
zsqfun=subs(z^2,[x,y,z],hypsol)
double(int(int(int(-intfac*zsqfun,s,slim1,slim2),...
t,0,2*pi),r,0,1))
zsqfun = 2*sinh(s)^2 ans = 3.2984e+003
Problem 2
Use a suitable three-dimensional change of variables to integrate the function

over the solid region between the upper sheet of the hyperboloid
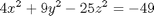
and the plane z = 3.
Additional Problems
1. Use a suitable change of variables to evaluate
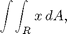
where R is the region in the first quadrant bounded by the lines y=2x, x=2y, and the hyperbolae xy=1 and xy=4.
2. In parametrizing the solid region inside a hyperboloid of one sheet, we started with a parametrization of the hyperboloid and introduced r, with limits of 0 and 1, as a factor of the first two coordinates, in order to parametrize the solid region.
(a) Verify that we would obtain the same answer for both the volume and the integral of z^2 if we made r a factor only of the first coordinate.
(b) Determine what would happen if we made r a factor of the third coordinate.
(c) Explain geometrically what you have demonstrated in parts (a) and (b).
3. Parametrize the tube of radius .5 around the trefoil parametrized by the input cell below. Refer to http://www.math.umd.edu/users/jmr/241/curves.html for details. Extend your parametrization to a solid tube by multiplying the terms involving the normal and binormal by a radial parameter.
trefoil=[(2+cos(3*t))*cos(2*t),(2+cos(3*t))*sin(2*t),cos(3*t)]
trefoil = [ cos(2*t)*(cos(3*t) + 2), sin(2*t)*(cos(3*t) + 2), cos(3*t)]
(a) Compute the volume of the tube. Compare your answer with the product of the length of the trefoil with the area of a typical normal disk. Do you think that what you observe is a coincidence? Explain.
(b) Integrate the square of the radial coordinate over the tube.
4. For the change of variables u = xy, v = x^2 - y^2, x > y > 0, compute the Jacobian of u and v with respect to x and y and also the inverse transformation and the Jacobian of x and y with espect to u and v. Verify that the Jacobians are inverses of one another.
5. (just for fun) This problem comes from the article "Sums of generalized harmonic series and volumes" by F. Beukers, J. Kolk, and E. Calabi, Nieuw Arch. Wisk. (4) 11 (1993), no. 3, 217--224. Show that the change of variables x = (sin u)/(cos v), y = (sin v)/(cos u), maps the triangle R bounded by the u and v axes and the line u + v = pi/2 to the square bounded by the x and y axes and the lines x = 1 and y = 1. Compute the Jacobian of the transformation and deduce that