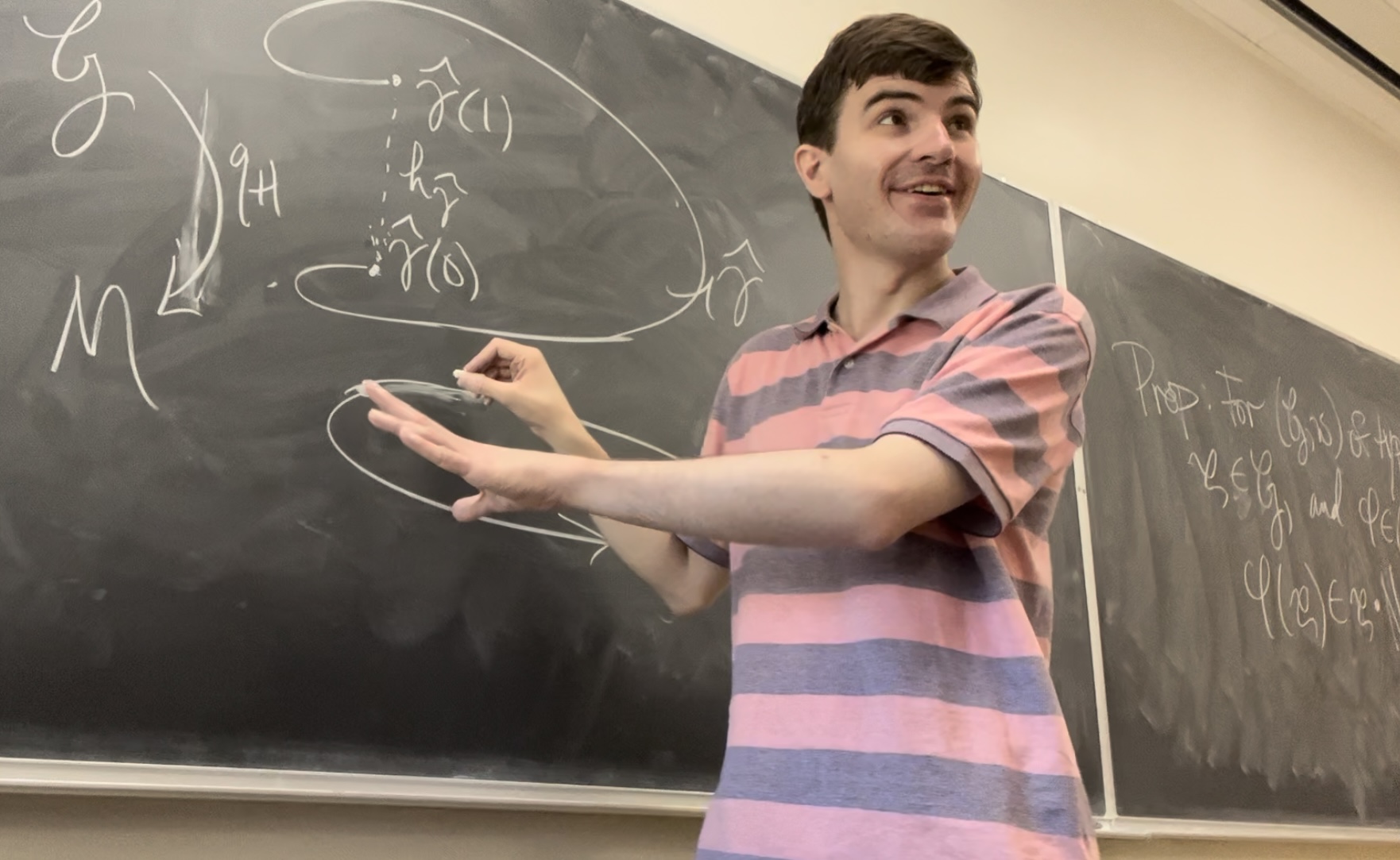Jacob W. Erickson
CV available here, last updated September 30, 2023
I'm a graduate student at the University of Maryland, College Park, studying under
Bill Goldman and Karin Melnick.
I'm interested in Lie groups, Cartan geometries,
and locally homogeneous geometric structures.
Papers
- Closed surface pairs with maximal local rolling symmetries
In preparation
This is my thesis.
- A stitching theorem for maps between Cartan geometries
In preparation
This will be a paper on the "stitching theorem" that I used in conjunction with sprawls
to prove that higher-order fixed points force compact projective geometries to be isomorphic to the Klein
geometry, if you went to my Strasbourg talk and are wondering where it is.
- A method for determining Cartan geometries from the local behavior of automorphisms
This is the "sprawl paper", if you went to my Strasbourg talk and are wondering where it is.
arXiv preprint
- Higher rank parabolic geometries with essential automorphisms and nonvanishing curvature
Transformation Groups vol 27 (2022)
arXiv preprint
- Intrinsic holonomy and curved cosets of Cartan geometries
European Journal of Mathematics vol 8, 446-474 (2022)
arXiv preprint
"Parabolic Geometries for People that Like Pictures"
(aka the Parabolic Geometries RIT)
During the Fall 2022 semester, I ran an RIT on parabolic geometries, with joint supervision from Bill Goldman.
The goal of the course was to present Cartan geometries---parabolic geometries in particular---in a more intuitive light,
with a heavy focus on visualization and pictures.
Below are some lecture notes from the course. We ended up focusing largely on understanding the models for Cartan geometries,
but I am in the process of filling out more of the course and compiling it into a book. A rough draft of the book (largely reproducing
these lecture notes) should be made available on AMS Open Math Notes soon. Until then, it is available
here.