Using Matlab for Exam 1
Contents
Initialization
format compact % omit blank lines
Problem 1(a)(b)
sol_a = dsolve('Dy+t*(y-1)^2=0,y(2)=-1') sol_b = dsolve('Dy+t*(y-1)^2=0,y(2)=1') ezplot(sol_a,[-3,3]); hold on ezplot(sol_b,[-3,3]); hold off; grid on
sol_a = 1/(t^2/2 - 5/2) + 1 sol_b = 1
numerical solution
f = @(t,y) -t*(y-1)^2; dirfield(f,-3:.2:3,-5:.2:3); hold on [t,y]=ode45(f,[2,10],-1); plot(t,y) % solve (a) for increasing t: stops at t=2.236 [t,y]=ode45(f,[2,-10],-1); plot(t,y) % solve (a) for decreasing t: stops at t=-2.235 [t,y]=ode45(f,[2,10],1); plot(t,y) % solve (b) for increasing t [t,y]=ode45(f,[2,-10],1); plot(t,y) % solve (b) for decreasing t hold off
Warning: Failure at t=2.236047e+00. Unable to meet integration tolerances without reducing the step size below the smallest value allowed (7.105427e-15) at time t. Warning: Failure at t=-2.235392e+00. Unable to meet integration tolerances without reducing the step size below the smallest value allowed (7.105427e-15) at time t.
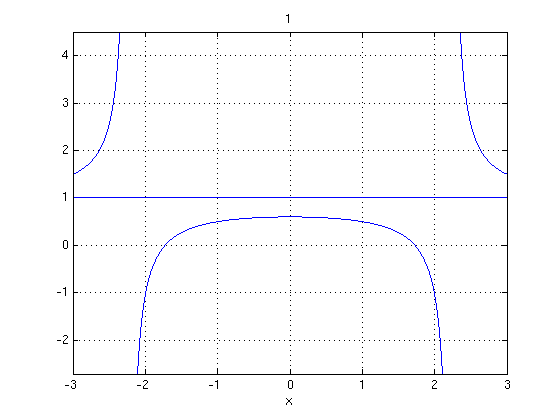
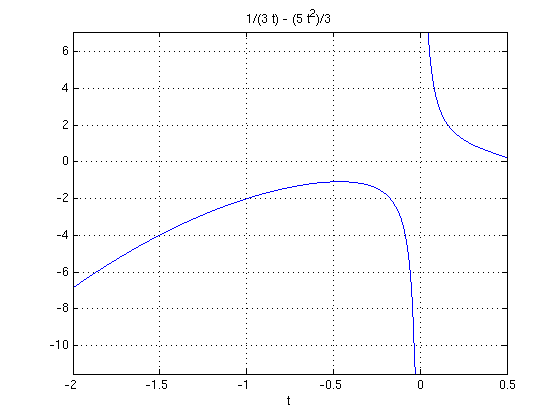
Problem 1(c)
sol = dsolve('Dy-2/t*y+1/t^2=0,y(-1)=-2','t') ezplot(sol,[-2,.5]); grid on
sol = 1/(3*t) - (5*t^2)/3
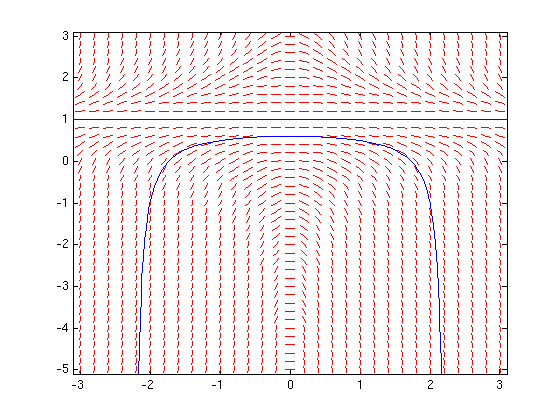
numerical solution
Here ode15s prints out a warning when the integration stops near zero. (ode45 does not print a warning, but only gives y-values for t up to zero).
f = @(t,y) 2/t*y-1/t^2; dirfield(f,-2:.1:.5,-8:.4:0); hold on [t,y]=ode15s(f,[-1,10],-2); plot(t,y) % solve ODE for increasing t: stops at t=0 [t,y]=ode15s(f,[-1,-10],-2); plot(t,y) % solve ODE for decreasing t hold off
Warning: Failure at t=-7.458341e-155. Unable to meet integration tolerances without reducing the step size below the smallest value allowed (2.649735e-169) at time t.
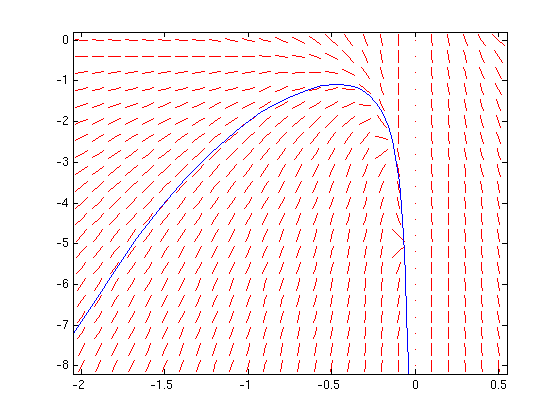
Problem 1(d)
Matlab version 2012b (which I use here) can solve this.
Older versions of Matlab (2010b, 2011b) cannot solve this. Using dsolve with initial condition gives "[ empty sym ]". One can get some answer by sol=dsolve('(2*y-4*t)*Dy-4*y+16*t=0','t');simplify(sol)
sol = dsolve('(2*y-4*t)*Dy-4*y+16*t=0,y(0)=-1','t')
sol = 2*t - (1 - 4*t^2)^(1/2)
numerical solution
solution exists for -.5 < t < .5
If solution stops at point with vertical slope ode15s works better than ode45. ode45 produces nonsense solution beyond interval where solution exists
f = @(t,y) (4*y-16*t)/(2*y-4*t); dirfield(f,-1:.1:1,-2:.2:2); hold on [t,y]=ode15s(f,[0,10],-1); plot(t,y) % solve ODE for increasing t: stops at t=.498 [t,y]=ode15s(f,[0,-10],-1); plot(t,y) % solve ODE for decreasing t: stops at t=-.495 hold off
Warning: Failure at t=4.975144e-01. Unable to meet integration tolerances without reducing the step size below the smallest value allowed (8.881784e-16) at time t. Warning: Failure at t=-4.954979e-01. Unable to meet integration tolerances without reducing the step size below the smallest value allowed (8.881784e-16) at time t.
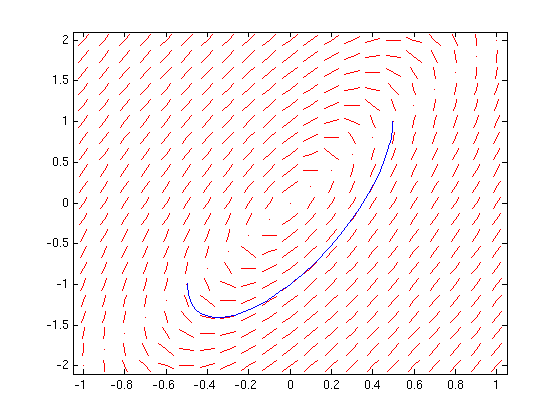
Problem 2
f = @(t,y) (y-1)*(y-2)*(y-4); dirfield(f,-1:.2:3,0:.2:4.5); hold on [t,y]=ode45(f,[1,10],1.5); plot(t,y) % solve (i) for increasing t [t,y]=ode45(f,[1,-10],1.5); plot(t,y) % solve (i) for decreasing t [t,y]=ode45(f,[1,10],3); plot(t,y) % solve (ii) for increasing t [t,y]=ode45(f,[1,-10],3); plot(t,y) % solve (ii) for decreasing t hold off
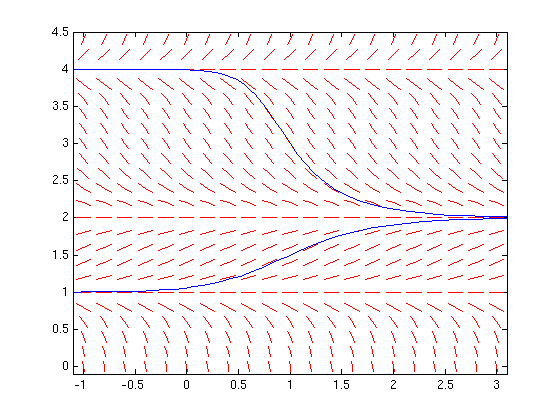
Problem 3
sol = dsolve('Dy=6-2*y/(10+t),y(0)=50','t') syms t; V = 10 + t; concentration = simplify(sol/V)
sol = 2*t + 3000/(t + 10)^2 + 20 concentration = 3000/(t + 10)^3 + 2
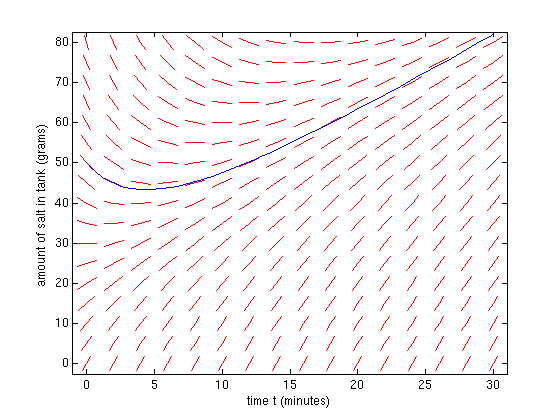
numerical solution
f = @(t,y) 6-2*y/(10+t); dirfield(f,0:2:30,0:5:80); hold on [t,y]=ode45(f,[0,30],50); plot(t,y) hold off xlabel('time t (minutes)'); ylabel('amount of salt in tank (grams)')