Using Matlab for Autonomous Systems

Here we consider the following example of an autonomous system:

y₁' = 4y₁ + y₂ + y₁ y₂

y₂' = y₁ + 4 y₂ + y₂²

Plotting the vector field and trajectories

First define the right hand side function g of the differential equation as

g = inline('[4*y(1)+y(2)+y(1)*y(2) ; y(1)+4*y(2)+y(2)^2]','t','y')

To plot the vector field for y₁ between -6 and 5 and y₂ between -6 and 1 type

vectfield(g,-6:.5:5,-6:.5:1)

To plot a trajectory in the phase plane starting at a point (a1, a2) at time t=0 for increasing values of t going from 0 to 4 type

[ts,ys] = ode45(g,[0,4],[a1;a2]); 
plot(ys(:,1),ys(:,2))

To plot the trajectory in the phase plane starting at the point (a1, a2) at time t=0 for decreasing values of t going from 0 to -4 type

[ts,ys] = ode45(g,[0,-4],[a1;a2]); 
plot(ys(:,1),ys(:,2))

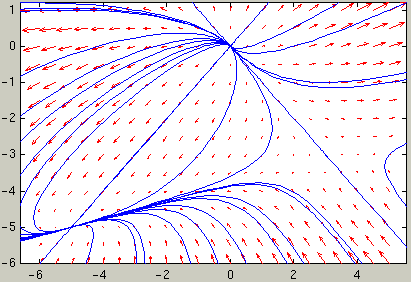
To get an idea of the behavior of the ODE, we plot the direction field and several trajectories together: We can choose e.g. the 35 starting points (a1, a2) with a1=-7,-5,-3,-1,1,3,5 and a2=-7,-5,-3,-1,1. From each of those points we plot the trajectory for t going from 0 to 4 and for t going from 0 to -4:

vectfield(g,-6:.5:5,-6:.5:1)
hold on 
for a1=-7:2:5   
  for a2=-7:2:1     
    [ts,ys] = ode45(g,[0,4],[a1;a2]); 
    plot(ys(:,1),ys(:,2))    
    [ts,ys] = ode45(g,[0,-4],[a1;a2]); 
    plot(ys(:,1),ys(:,2)) 
  end 
end

These commands will generate a number of warning messages (since some solutions don't exist for t in the whole interval [-4,4]) which you can ignore.

From the picture it appears that there are three critical points: A stable node, an unstable node, and a saddle point.

Investigation of critical points

It is convenient to define two functions g1(y1,y1), g2(y1,y2) containing the right-hand side functions as follows:

g1 = inline('4*y1+y2+y1*y2','y1','y2') 
g2 = inline('y1+4*y2+y2^2','y1','y2')

To find critical points where both g1 and g2 are zero we use solve:

syms y1 y2 
[y1s,y2s] = solve(g1(y1,y2),g2(y1,y2),y1,y2)

This returns

y1s =   [  0]
        [ -5] 
        [  3]  
   
y2s =   [  0] 
        [ -5] 
        [ -3]

Therefore we have found three critical points: (0,0), (-5,-5) and (3,-3).

To find the Jacobian matrix we type

jac = jacobian([g1(y1,y2);g2(y1,y2)],[y1,y2])

This returns the matrix

[   4+y2,   1+y1]
[      1, 4+2*y2]

As an example we will study the second critical point with coordinates y1s(2)=-5, y2s(2)=-5.

To evaluate the Jacobian at the critical point we substitute y1s(2) and y2s(2) for y1 and y2:

jac2 = subs(jac,{y1,y2},{y1s(2),y2s(2)})

which gives the matrix

[ -1, -4] 
[  1, -6]

To find the eigenvectors and eigenvalues of this matrix type

[eigvect,eigval] = eig(jac2)

which gives

eigvect =  [ 1, 4] 
           [ 1, 1]  
   
eigval =   [ -5,  0] 
           [  0, -2]

This means that the eigenvalues are -5 and -2. Hence this critical point is a stable node. The eigenvector for the first eigenvalue -5 is given by the first column of the matrix eigvect, it has components 1, 1. The eigenvector for the second eigenvalue -5 is given by the second column of the matrix eigvect, it has components 4, 1. Using the eigenvectors we can sketch by hand the behavior of the trajectories close to the critical point:

Compare this picture with the trajectories near (-5,-5) in the picture above.

You should try to analyze the other two critical two points by yourself in the same way.