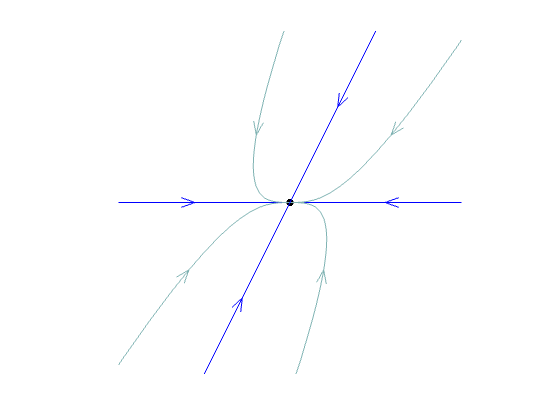
nodal sink
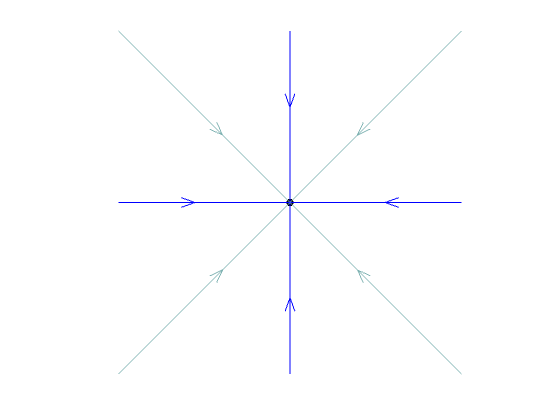
radial sink

twist sink (ccw)

spiral sink (cw)
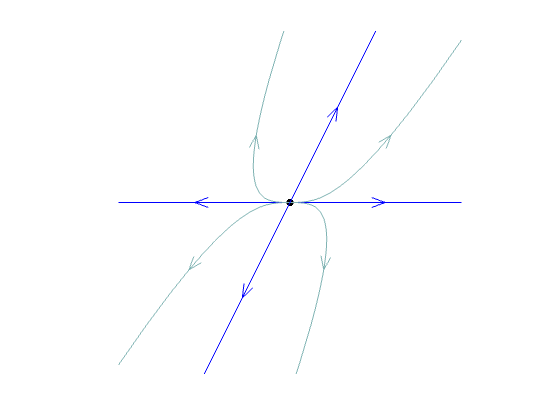
nodal source
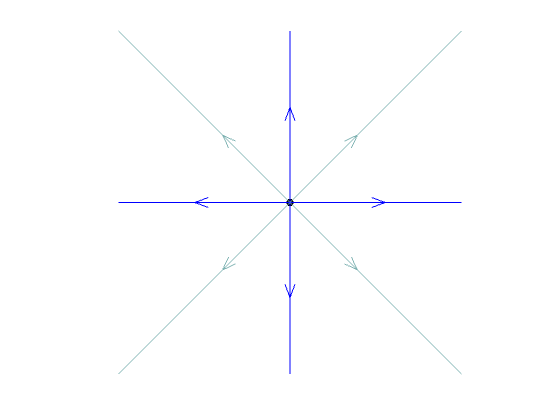
radial source

twist source (cw)

spiral source (ccw)
We say \( (x_*,y_*) \) is a stationary point if \( \left[ \matrix{f(x_*,y_*) \cr g(x_*,y_*)} \right] = \left[\matrix{0\cr0}\right]\), corresponding to a constant solution of the ODE.
The type and stability of the stationary point depends on the eigenvalues of the Jacobian matrix \[ A = \left[\matrix{\partial_xf(x_*,y_*) & \partial_yf(x_*,y_*) \cr \partial_xg(x_*,y_*) & \partial_y g(x_*,y_*)} \right] \]
| eigenvalues | linear ODE system | nonlinear ODE system | |||
|---|---|---|---|---|---|
| real | both pos. | different | nodal source | unstable, repelling | same |
| equal | radial source or twist source* | ||||
| both neg. | different | nodal sink | stable, attracting | ||
| equal | radial sink or twist sink* | ||||
| pos. and neg. | saddle | unstable, not repelling | |||
| nonreal | real part positive | spiral source | unstable, repelling | ||
| real part negative | spiral sink | stable, attracting | |||
| real part zero | center | stable, not attracting | ? | ||
*equal eigenvalues: If there are two eigenvectors we get a radial sink/source. If there is only one eigenvector (deficient case) we obtain a twist sink/source.
For twist sinks/sources, spiral sinks/sources and centers you should find out whether they are clockwise/counterclockwise. You can decide this by looking at the arrow at (1,0) (1st column of A), or the arrow at (0,1) (2nd column of A).
"same" means: type and stability for the nonlinear system are the same as for the corresponding linearized system:
Note: This page only considers the case of nonzero eigenvalues (i.e., matrix \(A\) is nonsingular). In this case both the linear and nonlinear ODE system have an isolated stationary point.
If all eigenvalues have
 nodal sink |
 radial sink |
 twist sink (ccw) |
 spiral sink (cw) |
 nodal source |
 radial source |
 twist source (cw) |
 spiral source (ccw) |
Remaining cases:
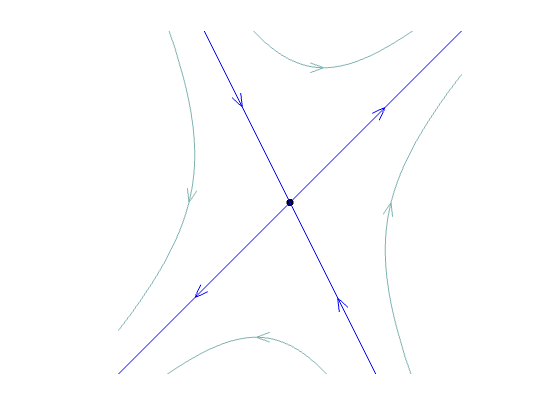 saddle (unstable, not repelling) |
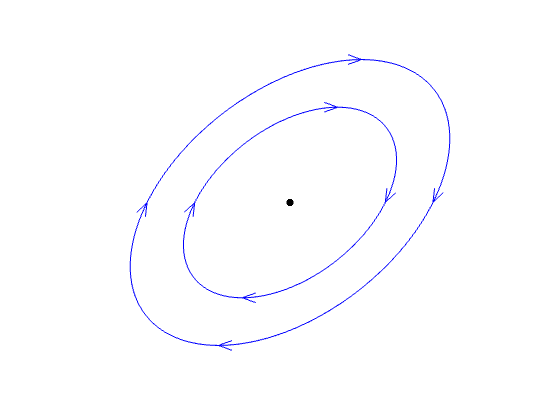 center (stable, not attracting, cw) |