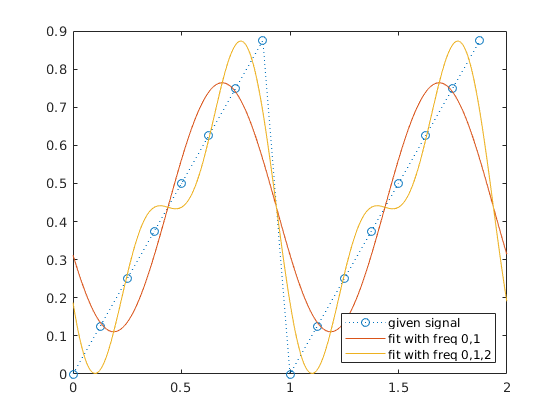
Least squares fit with functions 1,cos(2*pi*t),sin(2*pi*t),cos(4*pi*t),sin(4*pi*t)
Contents
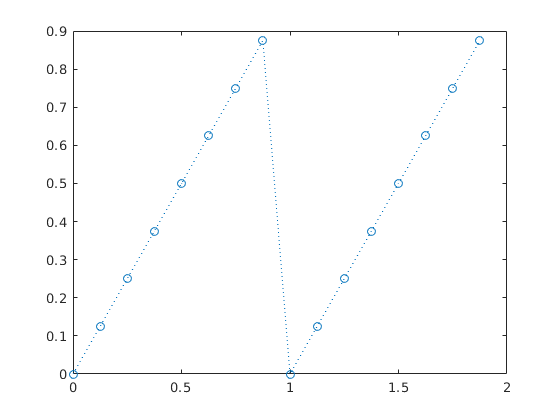
Given periodic signal
N = 8; t = (0:N-1)'/N; u = t; % "sawtooth signal" plot([t;t+1],[u;u],'o:') % plot two periods hold on
find coefficients of 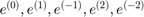
The discrete Fourier transform gives the vector ![$\hat u = [\hat u_0,\ldots ,\hat u_{N-1}]$](fourex1_eq05205155465878638182.png) .
.
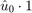 gives least squares fit with freq 0: using function 1
gives least squares fit with freq 0: using function 1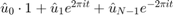 gives least squares fit with freq 0,1: using functions
gives least squares fit with freq 0,1: using functions 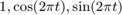
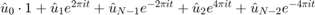 gives least squares fit with freq 0,1,2: using functions
gives least squares fit with freq 0,1,2: using functions 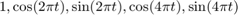
four = @(v) fft(v)/length(v); % define four, ifour ifour = @(v) ifft(v)*length(v); uh = four(u); % find discrete Fourier transform [uhat_0;...;uhat_7]
plot fitted curve
Note:  corresponds in Matlab to uh(1), uh(2), uh(3), ..., uh(N-1), uh(N).
corresponds in Matlab to uh(1), uh(2), uh(3), ..., uh(N-1), uh(N).
Np = 1000; % use 1000 points for plotting g(t) T = (0:Np-1)'/Np; U1 = uh(1) + uh(2)*exp(2*pi*i*T) + uh(N)*exp(-2*pi*i*T); % terms of freq 0,1 U2 = U1 + uh(3)*exp(4*pi*i*T) + uh(N-1)*exp(-4*pi*i*T); % terms of freq 0,1,2 plot([T;T+1],[U1;U1]) plot([T;T+1],[U2;U2]) hold off legend('given signal','fit with freq 0,1','fit with freq 0,1,2','Location','SE')