Optimal strategy for Rock, Paper, Scissors
Contents
Classic version of Rock, Paper, Scissors
Players C and R play rock, paper, scissors:
- player C picks rock, paper, scissors randomly with probabilities
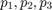
- player R picks rock, paper, scissors randomly with probabilities
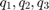
After each round the loser pays the winner 1$. This is is shown in the payoff matrix A: player C picks a column, player R picks a row
![$$ A = \left[ \matrix{0 & 1 & -1 \cr -1 & 0 & 1 \cr 1 & -1 & 0} \right] $$](game_ex_eq13247601952553748593.png)
Here the optimal strategy for each player is
- pick rock, paper, scissors with probability 1/3 each.
Then expected winnings for player C = expected loss for player R are zero, i.e., the game is fair.
A = [0 1 -1; -1 0 1; 1 -1 0] S = 2; Am = A + S; % add some S such that all entries of Am are positive % answer p,q,cost does not depend on choice of S b = [1;1;1]; c = [1;1;1]; [x,costm,y] = linearoptim(Am,b,c) p = x/sum(x) q = y/sum(y) costC = 1/sum(x) - S costR = 1/sum(y) - S cost = q'*A*p % expected winnings for player C = expected loss for player R
A =
0 1 -1
-1 0 1
1 -1 0
x =
0.16667
0.16667
0.16667
costm =
0.5
y =
0.16667
0.16667
0.16667
p =
0.33333
0.33333
0.33333
q =
0.33333
0.33333
0.33333
costC =
0
costR =
0
cost =
-6.163e-33
Rock, Paper, Scissors with modified payoffs
Now we play Rock, Paper, Scissors with a modified payoff matrix A:
- if player C wins with rock, paper, scissors, he gets 5$, 1$, 4$ respectively from player R
- if player R wins with rock, paper, scissors he gets 3$, 6$, 2$ respectively from player C
Now the optimal strategy is different:
- Player C: pick rock, paper, scissors with probabilities .392, .353, .255
- Player R: pick rock, paper, scissors with probabilities .608, .265, .127
Then expected winnings for player C = expected loss for player R are -.15686. Therefore the game is not fair, it is advantageous for player R.
A = [0 1 -2; -3 0 4; 5 -6 0] S = 10; Am = A + S; % add some S such that all entries of Am are positive % answer p,q,cost does not depend on choice of S [x,costm,y] = linearoptim(Am,b,c) p = x/sum(x) q = y/sum(y) costC = 1/sum(x) - S costR = 1/sum(y) - S cost = q'*A*p
A =
0 1 -2
-3 0 4
5 -6 0
x =
0.039841
0.035857
0.025896
costm =
0.10159
y =
0.061753
0.026892
0.012948
p =
0.39216
0.35294
0.2549
q =
0.60784
0.26471
0.12745
costC =
-0.15686
costR =
-0.15686
cost =
-0.15686