Contents
% Assignment 1 Solutions
Problem 1.
We use n=12 and obtain the equation 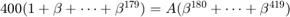 .
.
format compact % don't print blank lines between results b = 1.05^(-1/12); % (1+rho)^12 = 1 + r_eff pv_payments = 400*(1-b^180)/(1-b); % pv_withdraw = A*b^180*(1-b^240)/(1-b) % find A such that pv_payments = pv_withdraw: q = b^180*(1-b^240)/(1-b); A = pv_payments/q
A = 692.6079
Problem 2(a).
We use n=2 and obtain the equation 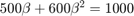 .
.
f = @(b) 500*b + 600*b^2 - 1000;
b = fzero(f,[0,1]); % Note: we can solve this with formula for quadratic equation
r_eff = b^-2 - 1
r_eff =
0.1320
Problem 2(b).
We use n=4 and obtain the equation 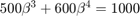 .
.
f = @(b) 500*b^3 + 600*b^4 - 1000; b = fzero(f,[0,1]); r_eff = b^-4 - 1
r_eff =
0.1136
Problem 2(c).
We use n=12 and obtain the equation 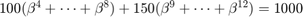 .
.
f = @(b) 100*b^4*(1-b^5)/(1-b) + 150*b^9*(1-b^4)/(1-b) - 1000; b = fzero(f,[0,.9999]); r_eff = b^-12 - 1
r_eff =
0.1455
Problem 3(a), Method 1
The probability for "heads" is p=0.4, the probability for "tails" is 1-p=0.6.
The random variable Y:=X4 can have the values 0,1,2,3,4. The probabilities are given by
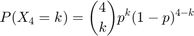
We then compute ![$E[Y] = \sum_{k=0}^4 P(Y=k)k$](ass1_sol_eq05412333161086712994.png) and
and ![$E[Y^2] = \sum_{k=0}^4 P(Y=k)k^2$](ass1_sol_eq14413674046886007703.png) .
.
Then ![$Var[Y] = E[Y^2] - E[Y]^2$](ass1_sol_eq14983236403128345436.png) .
.
p = 0.4; p4 = 1*p^4 % probability for Y=4 (4H, 0T) p3 = 4*p^3*(1-p) % probability for Y=3 (3H, 1T) p2 = 6*p^2*(1-p)^2 % probability for Y=2 (2H, 2T) p1 = 4*p*(1-p)^3 % probability for Y=1 (1H, 3T) p0 = (1-p)^4 % probability for Y=0 (0H, 4T) pv = [p0,p1,p2,p3,p4] % probabilities for the 5 cases Y=0,...,Y=4 Y = (0:4); % values of Y in these 5 cases EY = sum(pv.*Y) % E[Y] EY2 = sum(pv.*Y.^2) % E[Y^2] VarY = EY2 - EY^2 % Var[Y]
p4 =
0.0256
p3 =
0.1536
p2 =
0.3456
p1 =
0.3456
p0 =
0.1296
pv =
0.1296 0.3456 0.3456 0.1536 0.0256
EY =
1.6000
EY2 =
3.5200
VarY =
0.9600
Problem 3(a), Method 2
We start with the probabilities for X0: P(X0=0)=1. Then we compute the 2 probabilities for X1,..., then the 5 probabilities for X4.
Let Y:=X4, let U:=Y^2. We can then compute E[Y], E[U] by "method 2" explained in the course notes. We first compute the conditional expectations ![$E[Y\mid X_3=j]$](ass1_sol_eq10298916472318998549.png) for all
for all 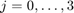 . Then we compute the conditional expectations
. Then we compute the conditional expectations ![$E[Y\mid X_2=j]$](ass1_sol_eq06873456895852253872.png) for all
for all 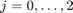 , etc.
, etc.
pv = 1; for k=1:4 fprintf('k=%g:\n',k) pv = 0.6*[pv,0] + 0.4*[0,pv] % probabilities for X_k=0,X_k=1,...,X_k=k end EY = (0:4); % conditional expectations for Y if X4=0,...,4 EU = (0:4).^2; % conditional expectations for U if X4=0,...,4 for k=3:-1:0 fprintf('k=%g:\n',k) EY = 0.6*EY(1:end-1) + 0.4*EY(2:end) % conditional expectations for Y if Xk=0,...,k EU = 0.6*EU(1:end-1) + 0.4*EU(2:end) % conditional expectations for U if Xk=0,...,k end VarY = EU - EY^2 % Var[Y]
k=1:
pv =
0.6000 0.4000
k=2:
pv =
0.3600 0.4800 0.1600
k=3:
pv =
0.2160 0.4320 0.2880 0.0640
k=4:
pv =
0.1296 0.3456 0.3456 0.1536 0.0256
k=3:
EY =
0.4000 1.4000 2.4000 3.4000
EU =
0.4000 2.2000 6.0000 11.8000
k=2:
EY =
0.8000 1.8000 2.8000
EU =
1.1200 3.7200 8.3200
k=1:
EY =
1.2000 2.2000
EU =
2.1600 5.5600
k=0:
EY =
1.6000
EU =
3.5200
VarY =
0.9600
Problem 3(b)
We obtain that ![$E[Z_1]=p$](ass1_sol_eq14667174403272981271.png) and
and ![$E[Z_1^2]=p$](ass1_sol_eq16601944419265712978.png) . Hence
. Hence
![$$Var[Z_1]=E[Z_1^2]-E[Z_1]^2=p-p^2=p(1-p).$$](ass1_sol_eq03315297991988441123.png)
Since 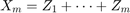 we obtain
we obtain ![$E[X_m]=E[Z_1]+\cdots+E[Z_m]=mp$](ass1_sol_eq13611127303090377377.png) .
.
Since the random variables  are independent we obtain
are independent we obtain
![$$Var[X_m] = Var[Z_1]+\cdots+Var[Z_m] = mp(1-p)$$](ass1_sol_eq09409379797454071948.png)
Note that we obtain for m=4 the same values as above.
p = 0.4; EZ1 = (1-p)*0 + p*1 % E[Z1] = p EZ12 = (1-p)*0^2 + p*1^2; % E[Z1^2] = p VarZ1 = EZ12 - EZ1^2 % Var[Z1] = p - p^2 EY = 4*EZ1 VarY = 4*VarZ1
EZ1 =
0.4000
VarZ1 =
0.2400
EY =
1.6000
VarY =
0.9600
Problem 3(c)
Find the conditional expectation of X4 under the condition X1=1.
We have 16 possible outcomes: 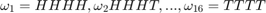 . We have the probabilities
. We have the probabilities 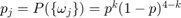 if
if  contains k times heads and (4-k) times tails.
contains k times heads and (4-k) times tails.
The expectation E[Y] is given by 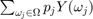 .
.
For an event 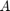 the conditional expectation is given by
the conditional expectation is given by
![$$E[Y\mid A] = \frac{E[1_A\cdot Y]}{P(A)} =\frac{\sum_{\omega_j\in A} p_j\cdot Y(\omega_j)}{\sum_{\omega_j\in A} p_j}$$](ass1_sol_eq13966917319763972817.png)
Here A is the event 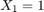 . Hence the first toss must be "heads" and A consists of the 8 outcomes H*** where each "*" is either H or T.
. Hence the first toss must be "heads" and A consists of the 8 outcomes H*** where each "*" is either H or T.
Therefore the possible values for 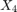 are
are 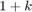 where
where 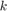 is the number of "heads" in the last three tosses. Hence
is the number of "heads" in the last three tosses. Hence
![$$E[X_4 \mid X_1=1] = 1 + E[X_3] = 1 + 3p = 2.2$$](ass1_sol_eq06352830004202096029.png)
Method 2: In Problem 3(a), Method 2 we computed actually all conditional expectations ![$E[Y\mid X_k=j]$](ass1_sol_eq15019427161564504613.png) for all
for all 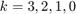 and
and 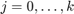 . Therefore we look at the output above: for k=1 we see the two values
. Therefore we look at the output above: for k=1 we see the two values ![$E[Y\mid X_1=0] = 1.2$](ass1_sol_eq16935766640811424093.png) and
and ![$E[Y\mid X_1=1] = 2.2$](ass1_sol_eq13655024762231471697.png) .
.