Example for Euler method

Contents

You need to download an m-file

You have to download the m-file dirfield.m.

function euler_demo

format short g

Initial value problem

We consider the initial value problem

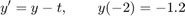
$$y'=y-t,\qquad y(-2)=-1.2$$

and we want to find the solution y(t) for t in [-2,1].

We use ode45 to find the solution of the initial value problem and obtain the approximation -2.01711 for y(T).

We plot the solution together with the direction field.

f = @(t,y) y-t;                   % define function f(t,y)
dirfield(f,-2:.2:1, -2:.2:0.2); hold on

t0 = -2;  y0 = -1.2;              % initial point
T = 1;                            % final t-value
[ts,ys] = ode45(f,[t0,T],y0);     % solve IVP

yfinal = ys(end);                 % value for y at time T
fprintf('y(T) = %g\n',yfinal)

plot(ts,ys,'b')                   % plot solution
title('Solution of IVP')

y(T) = -2.01711

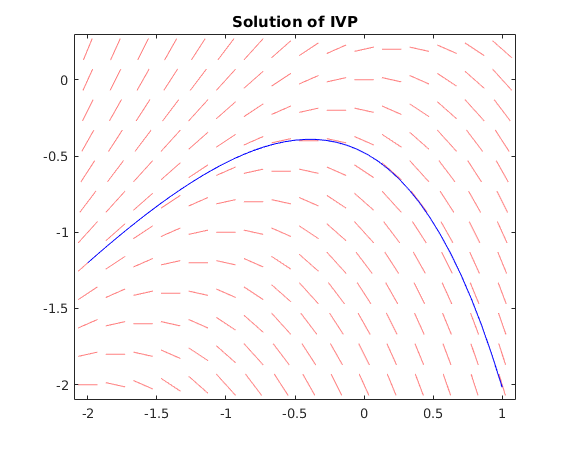
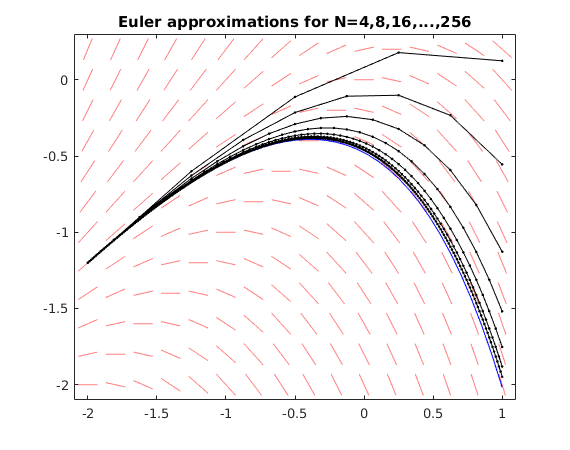
Use Euler method with N=4,8,16,...,256

We see that the Euler approximations get closer to the correct value y(T)=-2.01711 as N increases.

When we double the value of N the error gets divided by about 2. This means that the error is bounded by 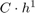$C\cdot h^1$: The Euler method converges with order $h^1$.

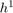olderr = NaN;
for N = 2.^(2:8)
  [ts,ys] = Euler(f,[t0,T],y0,N);
  err = ys(end)-yfinal;           % error
  fprintf('N = %3g, approx.for y(T) = %10g, error = %10g, quotient = %g\n',N,ys(end),err,olderr/err)
  olderr = err;
  plot(ts,ys,'k.-')               % plot Euler solution
end
hold off
title('Euler approximations for N=4,8,16,...,256')

N =   4, approx.for y(T) =   0.124219, error =    2.14133, quotient = NaN
N =   8, approx.for y(T) =  -0.555357, error =    1.46176, quotient = 1.4649
N =  16, approx.for y(T) =   -1.12729, error =   0.889824, quotient = 1.64275
N =  32, approx.for y(T) =   -1.51891, error =   0.498202, quotient = 1.78607
N =  64, approx.for y(T) =   -1.75231, error =   0.264799, quotient = 1.88143
N = 128, approx.for y(T) =   -1.88043, error =   0.136683, quotient = 1.93732
N = 256, approx.for y(T) =   -1.94765, error =  0.0694635, quotient = 1.9677

code of function Euler(f,[t0,T],y0,N)

At each step we evaluate the slope s=f(t,y) and then update y=y+s*h, t=t+h.

function [ts,ys] = Euler(f,tv,y0,N);
  t0 = tv(1); T = tv(2);
  h = (T-t0)/N;                    % stepsize h
  ts = zeros(N+1,1); ys = zeros(N+1,1);
  t = t0; y = y0;                  % initial point
  ts(1) = t; ys(1) = y;

  for i=1:N
    s = f(t,y);                    % evaluate direction field at current point
    y = y + s*h;                   % follow line with slope s from t to t+h
    t = t + h;
    ts(i+1) = t; ys(i+1) = y;      % store result in vectors ts,ys
  end
end

end


Published with MATLAB® R2017a