Optimization: Function of 1 variable
Contents
Example function
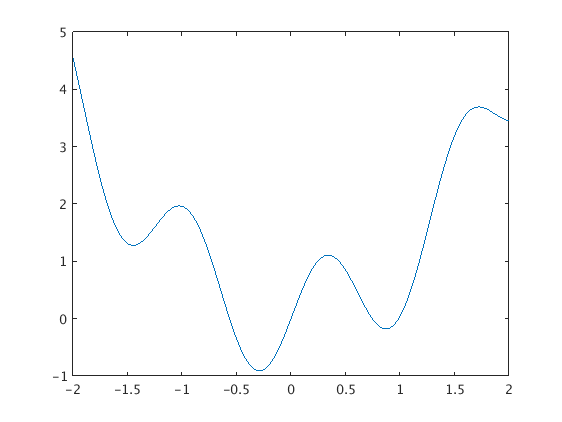
We want to find a local minimum of f(x) = sin(5x)+x^2. This function has several local minima.
f = @(x) sin(5*x) + x.^2;
X = -2:.01:2;
plot(X,f(X)); hold on
Using fminbnd
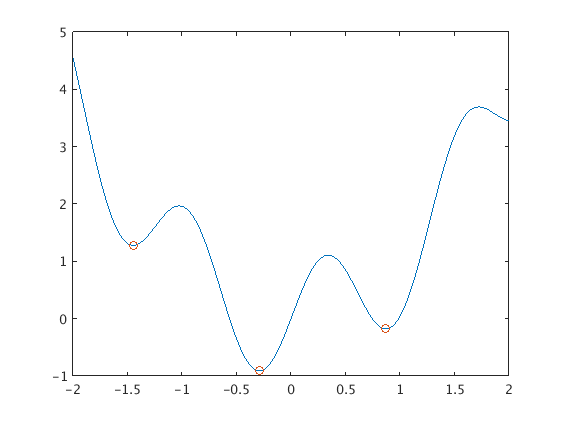
x = fminbnd(f,a,b) finds a local minimum in a given interval [a,b].
We obtain the minimal function value -0.9086 at the point x2 = -0.2908.
x1 = fminbnd(f,-2,-1) % find local minimum in [-2,-1] y1 = f(x1) x2 = fminbnd(f,-1,0) % find local minimum in [-1,0] y2 = f(x2) x3 = fminbnd(f,0,1) % find local minimum in [0,1] y3 = f(x3) plot([x1,x2,x3],[y1,y2,y3],'o') hold off
x1 =
-1.44731477377014
y1 =
1.2793381542907
x2 =
-0.290839136231191
y2 =
-0.908622439871121
x3 =
0.871286039172192
y3 =
-0.178173431577195