Interpolation: Find good approximation from given samples

Contents

Example: signal with discontinuity, exponential decay

As an example we use the function

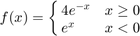
$$ f(x) = \cases{4e^{-x} & $x\ge 0$ \cr e^x & $x<0$ }$$

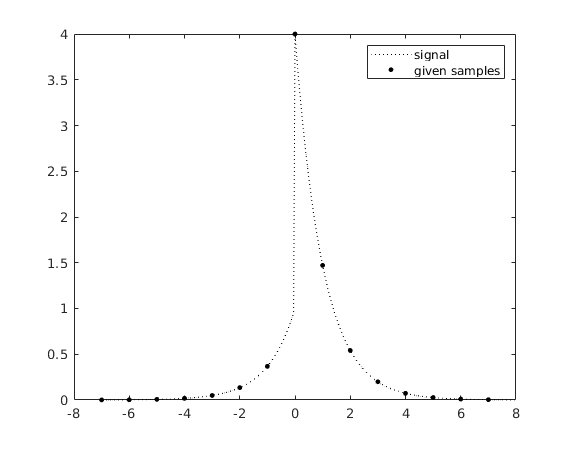
Here we use 15 points with a spacing of h=1.

fct = @(x) 4*exp(-x).*(x>=0) + exp(x).*(x<0);

a = -7;
b = 7;
N = 15;                 % number of given points
h = (b-a)/(N-1)         % spacing
x = a + (0:N-1)*h;      % N equidistant nodes where values are given
                        % same as linspace(a,b,N)
F = fct(x);             % discrete signal

m = 20;                 % "upsampling factor": we want to approximate
                        % function at points with spacing h/m
xf = a + (0:m*N-1)*h/m; % points with spacing h/m

plot(xf,fct(xf),'k:',x,F,'k.','MarkerSize',11); hold on
legend('signal','given samples')

h =
     1

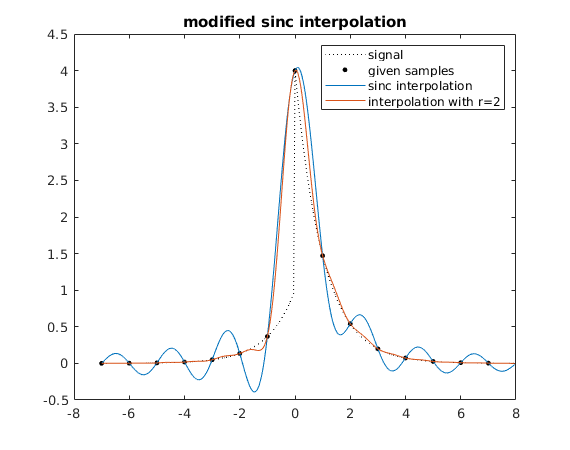
Sinc interpolation

The discrete values 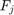$F_j$ correspond to a linear combination of Dirac deltas

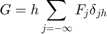
$$ G = h \sum_{j=-\infty} F_j \delta_{jh}$$

The Fourier transform is the 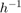$h^{-1}$-periodic function 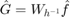$\hat G = W_{h^{-1}}\hat f$, i.e.,

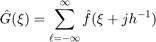
$$\hat G(\xi) = \sum_{\ell=-\infty}^\infty \hat f(\xi + j h^{-1})$$

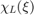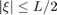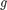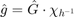Let $\chi_L(\xi)$ denote the function which is 1 for $|\xi|\le L/2$, zero otherwise. We define the interpolating function $g$ by $\hat g = \hat G\cdot \chi_{h^{-1}}$ (low pass filter). Hence the interpolating function is the convolution 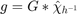$g = G * \hat\chi_{h^{-1}}$. Since 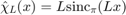$\hat\chi_L(x) = L \mathrm{sinc}_\pi(L x)$ we obtain the "Sinc Interpolation Formula"

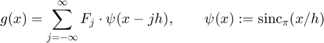
$$ g(x) = \sum_{j=-\infty}^\infty F_j \cdot \psi(x-jh), \qquad \psi(x):=\mathrm{sinc}_\pi(x/h)$$

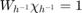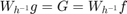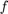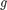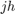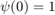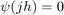Note that $W_{h^{-1}}\chi_{h^{-1}}=1$, hence $W_{h^{-1}}g = G = W_{h^{-1}}f$. Therefore sampling $f$ and $g$ at the points $jh$ gives the same values. This corresponds to the fact that $\psi(0)=1$ and $\psi(jh)=0$ for nonzero integers $j$.

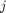Note that the discontinuity of the signal causes large oscillations in the interpolating function (Gibbs phenomenon). This is due to the fact that 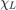$\chi_L$ is discontinuous, so 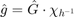$\hat g = \hat G\cdot \chi_{h^{-1}}$ has jumps, and 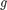$g$ has slow decay.

t = (-N*m:N*m)/m*h;
psi = sinc(t/h);
Fu = upsample(F,m);     % Fu = [F(1),0,...,0,F(2),0,...,0,...]
                        % put m-1 zeros after every F(j), Fu has length N*m

                        % conv(Fu,s) computes discrete convolution
                        % conv(Fu,s,'same') gives only values where Fu is given
G = conv(Fu,psi,'same'); % G has length N*m (because of 'same')
xf = a + (0:m*N-1)*h/m;
plot(xf,G)
legend('signal','given samples','sinc interpolation')
title('sinc interpolation')

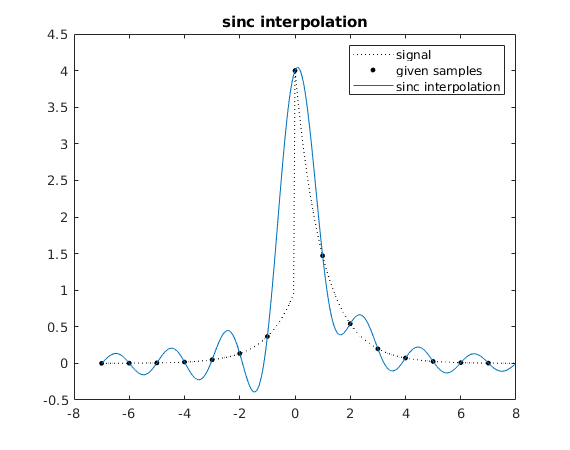
Modified Sinc Interpolation: Use "smoother low pass filter" in frequency domain

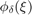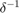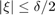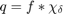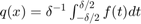Let $\phi_\delta(\xi)$ denote the function which is $\delta^{-1}$ for $|\xi|\le \delta/2$, zero otherwise. Note that the convolution $q=f*\chi_\delta$ gives the "moving average" $q(x)=\delta^{-1}\int_{-\delta/2}^{\delta/2}f(t)dt$.

Let 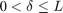$0<\delta\le L$. Then the convolution 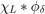$\chi_L*\phi_\delta$ is piecewise linear and continuous (the derivative has jumps). Its Fourier transform is

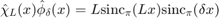
$$\hat\chi_L(x) \hat\phi_\delta(x) = L\mathrm{sinc}_\pi(Lx)\mathrm{sinc}_\pi(\delta x)$$

Let 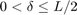$0<\delta\le L/2$. Then the convolution 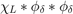$\chi_L*\phi_\delta*\phi_\delta$ is piecewise quadratic with a continous derivative (the second derivative has jumps). Its Fourier transform is

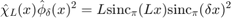
$$\hat\chi_L(x) \hat\phi_\delta(x)^2 = L\mathrm{sinc}_\pi(Lx)\mathrm{sinc}_\pi(\delta x)^2$$

We now use instead of 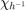$\chi_{h^{-1}}$ the smoother function 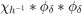$\chi_{h^{-1}}*\phi_\delta*\phi_\delta$. This gives the "Modified Sinc Interpolation Formula"

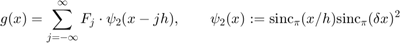
$$ g(x) = \sum_{j=-\infty}^\infty F_j \cdot \psi_2(x-jh), \qquad \psi_2(x):=\mathrm{sinc}_\pi(x/h)\mathrm{sinc}_\pi(\delta x)^2$$

We use the largest value 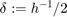$\delta:=h^{-1}/2$:

r = 2;                  % use r=2 steps of smoothing: low pass filter chi_L*phi_delta*phi_delta
delta = (1/h)/r;        % we need 0 < delta <= (1/h)/r. We choose largest value.

psir = sinc(t/h).*sinc(delta*t).^r;
Gr = conv(Fu,psir,'same');
plot(xf,Gr);

title('modified sinc interpolation')
legend('signal','given samples','sinc interpolation','interpolation with r=2')


Published with MATLAB® R2018a