Smoothing and Cutoff Functions
Contents
You need to download m-files
You need to download the files Phi.m and Chi.m. Put them in the same directory as your other m-files.
Why use "smooth cutoff functions"
If we only want to use values of  for
for ![$x\in [-M,M]$](smoothing_eq09540398038694735737.png) we could use
we could use  inside this interval, and zero outside. But this gives a function with jumps, and the Fourier transform has oscillations and slow decay like
inside this interval, and zero outside. But this gives a function with jumps, and the Fourier transform has oscillations and slow decay like 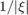 (Gibbs phenomenon).
(Gibbs phenomenon).
In several applications we can avoid this problem by using smoother cutoff functions.
- reconstructing a function
 from the Fourier transform
from the Fourier transform  for
for 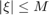 .
. - reconstructing a function
 from samples
from samples  .
. - "short time Fourier transform": analyzing the time dependent behavior of frequencies. We multiply the signal
 with "windowing functions"
with "windowing functions" 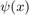 ,
, 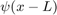 ,
,  , ... and then compute the Fourier transform of each term
, ... and then compute the Fourier transform of each term 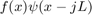 . Since the windowing functions
. Since the windowing functions 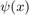 ,
, 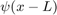 ,
,  , ... add up to 1 we can reconstruct the original signal from the Fourier transforms of each term.
, ... add up to 1 we can reconstruct the original signal from the Fourier transforms of each term.
Smoothing by convolution
The moving average over an interval of length delta corresponds to convolution with 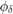 .
.
Applying this n times corresponds to convolution with the function  (convolution of n terms
(convolution of n terms 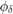 ).
).
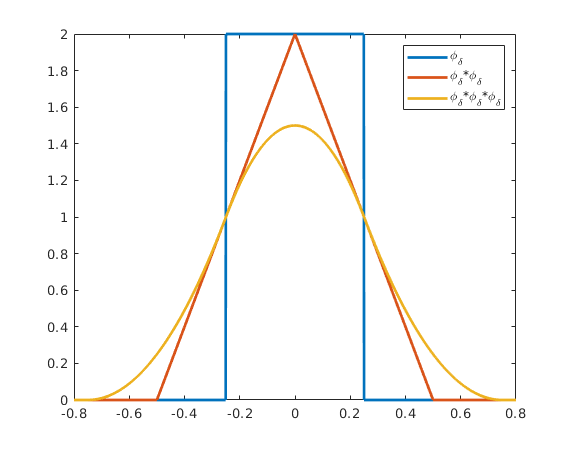
As an example we use delta=.5 and plot the functions 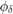 ,
,  ,
, 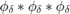 .
.
All three functions have integral 1.
In Matlab we use phi(x/delta,n)/delta for  . The Fourier transform is
. The Fourier transform is  .
.
d = .5; % delta=.5 x = -.8:.001:.8; plot( x,Phi(x/d)/d, x,Phi(x/d,2)/d, x,Phi(x/d,3)/d ,'LineWidth',2); legend('\phi_\delta','\phi_\delta*\phi_\delta','\phi_\delta*\phi_\delta*\phi_\delta'); axis tight
Cutoff functions: simplest choice
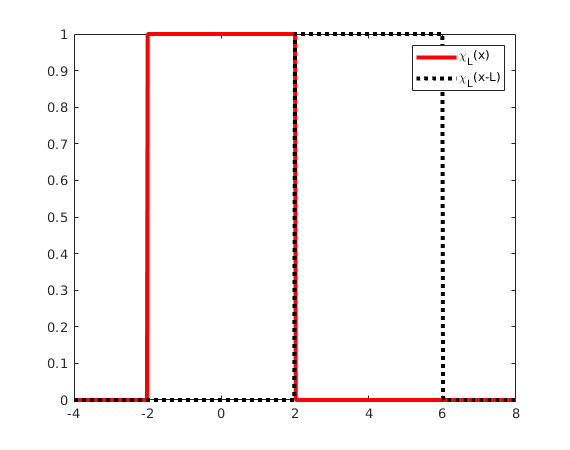
The function 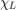 is 1 for
is 1 for  , zero otherwise.
, zero otherwise.
Here we show for  the functions
the functions  , and
, and  . If we add all shifts by integer multiples of
. If we add all shifts by integer multiples of  we get the constant function 1.
we get the constant function 1.
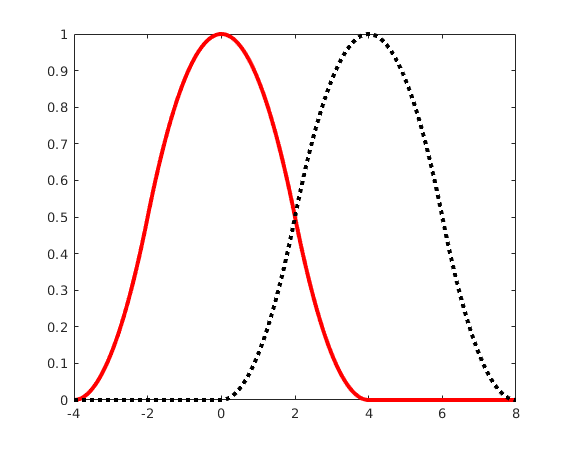
L = 4; x = -4:.02:8; plot( x,Chi(x,L),'r',x,Chi(x-L,L),'k:','LineWidth',3); legend('\chi_L(x)','\chi_L(x-L)')
Cutoff functions: smoothing with 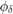
Now we use the function 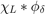 which is piecewise linear and is continuous. This function is zero outside of
which is piecewise linear and is continuous. This function is zero outside of ![$[(-L-\delta)/2,(L+\delta)/2]$](smoothing_eq07382433342877852411.png) . It is one in the interval
. It is one in the interval ![$[(-L+\delta)/2,(L-\delta)/2]$](smoothing_eq10155851774575315577.png) .
.
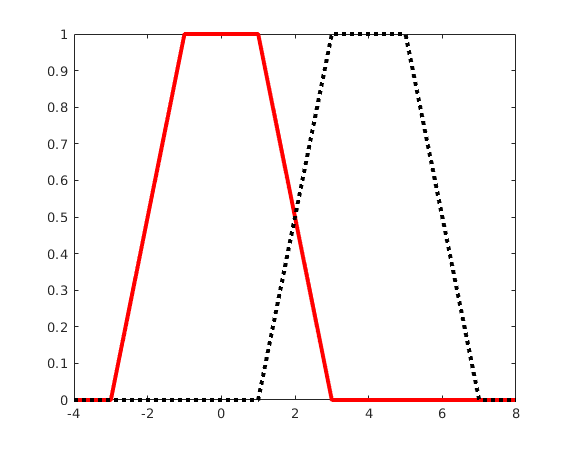
Here we show for  and
and  the functions
the functions  , and the function shifted by
, and the function shifted by  . If we add all shifts by integer multiples of
. If we add all shifts by integer multiples of  we get the constant function 1.
we get the constant function 1.
L = 4; d = 2; x = -4:.02:8; plot( x,Chi(x,L,d),'r',x,Chi(x-L,L,d),'k:','LineWidth',3);
Cutoff functions: smoothing with 
Now we use the function  which is piecewise quadratic, and has a continuous derivative. This function is zero outside of
which is piecewise quadratic, and has a continuous derivative. This function is zero outside of ![$[-L/2-\delta,L/2+\delta]$](smoothing_eq05340807168335882991.png) . It is one in the interval
. It is one in the interval ![$[-L/2+\delta,L/2-\delta]$](smoothing_eq12923839931535866466.png) .
.
Here we show for  and
and  the functions
the functions  , and the function shifted by
, and the function shifted by  . If we add all shifts by integer multiples of
. If we add all shifts by integer multiples of  we get the constant function 1.
we get the constant function 1.
Chi(x,L,delta,n) gives the function  (
( times
times 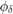 ). Its Fourier transform is
). Its Fourier transform is  .
.
L = 4; d = 1; x = -4:.02:8; plot( x,Chi(x,L,d,2),'r',x,Chi(x-L,L,d,2),'k:','LineWidth',3);
Cutoff functions: smoothing with  , largest choice of
, largest choice of 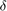
For Chi(x,L,delta,n) we need  .
.
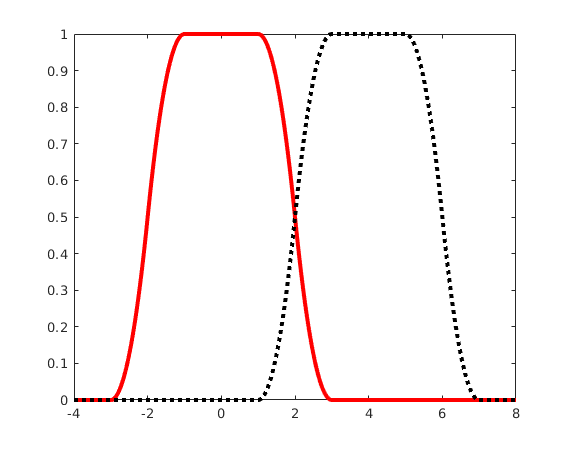
We again use  and
and  , but now we choose the largest possible value
, but now we choose the largest possible value  . If we add all shifts by integer multiples of
. If we add all shifts by integer multiples of  we get the constant function 1.
we get the constant function 1.
L = 4; d = 2; x = -4:.02:8; plot( x,Chi(x,L,d,2),'r',x,Chi(x-L,L,d,2),'k:','LineWidth',3);