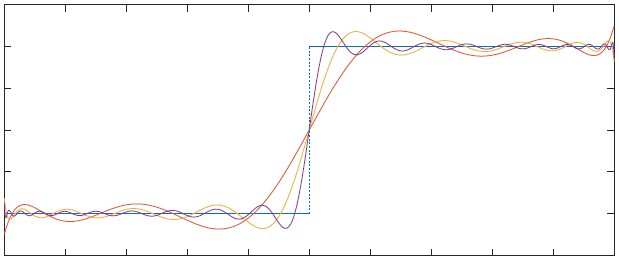
 |
| Least squares approximation of sign(x) on [-1,1] with polynomials of degree 10,20,40 |
We will use Matlab to see how various algorithms perform (or fail).
Matlab can be downloaded for free from TERPware.
How to hand in Matlab results for homeworks: