Example for Principal Component Analysis: Olympic Decathlon 1988
Contents
Read Data Set
This data set contains the results of the 1988 olympic decathlon competition. Each athlete competes in 10 events:
- running: 100m, 110m hurdles, 400m, 1500m
- jumping: long jump, high jump, pole vault
- throwing: javelin, discus, shot put
We want to understand how the athletes differ from each other:
- Are there e.g. athletes which are good at throwing, but bad at jumping (or vice versa)?
- Which events give very similar results (e.g. running 100m and 400m)?
- In which events do the top finishers excel?
We denote the 33 athletes by R1,...,R33 according to their final result (total of the points in 10 events): R1, R2, R3 won gold, silver, bronze.
Each of the 33 athlete was awarded points in 10 events, so we have 33 data points in R^10. Since we cannot make a plot in R^10 we want to find the 2-dimensional subspace which is closest to the data points. We can then plot the orthogonal projection of the data points onto this 2-dimensional subspace.
T = readtable('decathlon1988s.txt','Delimiter','\t','HeaderLines',6,'ReadRowNames',true) % 'Table' data type in Matlab data = table2array(T); % numbers as Matlab array athletenames = T.Properties.RowNames; % cell arrays of athlete names and event names eventnames = T.Properties.VariableNames; [m,n] = size(data);
T =
33×10 table
r100m longjmp shotput highjmp r400m r110m discus polevlt javelin r1500m
_____ _______ _______ _______ _____ _____ ______ _______ _______ ______
R1 806 918 819 1061 866 834 855 819 758 752
R2 890 922 788 776 923 916 754 941 764 725
R3 821 920 741 776 895 873 739 972 801 790
R4 947 905 791 831 858 884 763 880 799 648
R5 899 965 703 915 893 951 727 880 621 718
R6 856 918 662 776 936 924 689 972 700 835
R7 821 826 736 859 845 925 699 1132 762 611
R8 850 802 811 803 899 929 691 849 783 772
R9 827 842 760 831 854 891 713 880 835 747
R10 810 881 805 776 880 879 829 972 730 605
R11 874 950 811 776 817 942 702 849 838 584
R12 821 896 758 749 860 836 715 819 826 834
R13 856 883 662 859 898 854 655 910 690 826
R14 863 903 704 776 917 886 744 702 837 751
R15 854 922 741 776 869 797 699 819 798 761
R16 841 833 760 831 820 876 730 880 696 754
R17 761 755 856 803 757 726 884 849 932 546
R18 738 814 827 749 822 845 801 880 741 643
R19 845 823 692 749 911 912 672 849 611 795
R20 885 830 841 619 829 857 773 880 745 522
R21 748 900 724 749 815 774 641 790 844 768
R22 755 818 716 831 787 823 646 819 752 798
R23 778 833 747 803 804 853 794 731 673 727
R24 795 807 681 944 816 804 639 790 653 694
R25 861 869 676 831 827 854 625 760 630 646
R26 789 774 584 859 891 803 614 790 669 744
R27 838 809 648 670 879 834 625 819 581 799
R28 750 816 739 749 762 828 784 790 682 542
R29 804 790 631 696 898 777 624 731 628 731
R30 753 835 664 644 849 783 712 760 641 596
R31 767 635 727 723 758 746 791 790 705 589
R32 759 682 626 749 801 850 639 617 697 596
R33 738 859 502 723 782 710 551 645 662 745
Perform Principal Component Analysis
We see that
- the first principal component captures 33.8% of the variance
- the first 2 principal components capture 59.2% of the variance
- the first 3 principal components capture 71.2% of the variance
Z = data'; % use transpose matrix: columns of Z are event values for each athlete % We obtain 33 data points in R^10 X = Z - mean(Z,2)*ones(1,m); % subtract the row mean from each row Variance = norm(X,'fro')^2 % Variance is 33 times the variance of the data [U,S,V] = svd(X); s = diag(S) % singular values Variance2 = sum(s.^2) % same as Variance cumsum(s.^2)/sum(s.^2) % amount of variance which is captured by 1,2,3,... principal components
Variance =
1.8799e+06
s =
797.5138
690.4129
474.4599
429.3924
357.2134
297.3019
258.1165
184.9458
165.8706
115.8598
Variance2 =
1.8799e+06
ans =
0.3383
0.5919
0.7116
0.8097
0.8776
0.9246
0.9600
0.9782
0.9929
1.0000
First two principal components
We choose the columns of U as the new basis of our 10-dimensional data space. This is an orthonormal change of basis: c = U'*x.
For our data points we obtain C = U'*X = S*V.
We then plot the projection of the data points onto the span of the first two columns u1,u2.
Each of the data points is approximated by c1*u1 + c2*u2, and we plot the points (c1,c2).
The horizontal green line corresponds to the best 1-dimensional subspace approximating the data.
The original unit vectors in the 10-dimensional data space (for events) become after the projection the columns of U(:,1:2)', i.e., the first two rows of U. We plot these vectors in red (with a scaling factor so that we can see them).
C = S(1:2,1:2)*V(:,1:2)'; % (c1,c2) coordinates of data points, same as U(:,1:2)'*X W = 600*U(:,1:2); % projected unit vectors, scaled with factor 600 plot(C(1,:),C(2,:),'o'); hold on % plot (c1,c2) text(C(1,:),C(2,:),athletenames,'FontSize',7,'VerticalAlignment','bottom'); % label with athlete name z = zeros(1,n); plot([z;W(:,1)'],[z;W(:,2)'],'r'); % plot projected unit vectors for events, label with event names text(W(:,1),W(:,2),eventnames,'FontSize',7,'VerticalAlignment','bottom','HorizontalAlignment','right','color','red'); grid on; axis equal xtotvec = ones(n,1)/sqrt(n); % unit vector for finding sum of points Wtot = 600*U(:,1:2)'*xtotvec; % plot([0;Wtot(1)],[0;Wtot(2)],'k:'); % plot vector for "total" ax = axis; plot(ax(1:2),[0 0],'g',[0 0],ax(3:4),'g') % draw horizontal and vertical axes in green xlabel('c_1'); ylabel('c_2') hold off
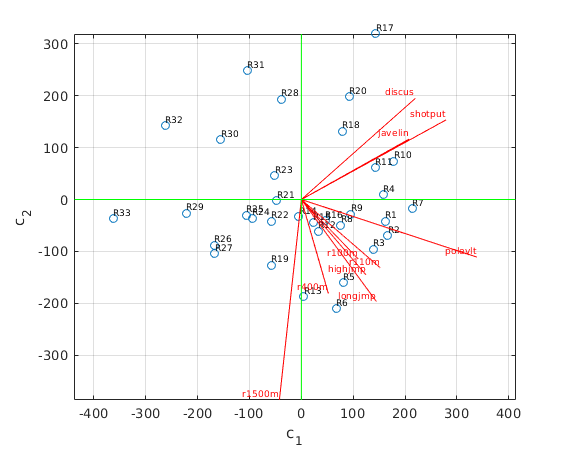
Interpretation of the result
- The first principal component c1 (along horizontal green line) increases most strongly with pole vault, shotput, discus, javelin , and decreases with 1500m. Note that the first principal component is closely related to the total score (the sum of all points, i.e., the inner product of the score vector with the vector (1,...,1)). We see that the top finishers R1, R2, R3, ... are on the right, and the bottom finishers R31, R32, R33 are on the left.
- The second principal component c2 (along vertical green line) increases with the throwing events, and decreases most strongly with 1500m.
First three principal components
We now use the first three principal components and plot the points (c1,c2,c3).
We show two "side views" of this 3d picture: c3 vs c1, and c3 vs c2.
C = S(1:3,1:3)*V(:,1:3)'; % (c1,c2,c3) coordinates of data points, same as U(:,1:3)'*X W = 600*U(:,1:3); % projected unit vectors, scaled with factor 600 figure(1) % plot (c1,c3) plot(C(1,:),C(3,:),'o'); hold on text(C(1,:),C(3,:),athletenames,'FontSize',7,'VerticalAlignment','bottom'); z = zeros(1,n); plot([z;W(:,1)'],[z;W(:,3)'],'r'); % plot projected unit vectors for events text(W(:,1),W(:,3),eventnames,'FontSize',7,'VerticalAlignment','bottom','HorizontalAlignment','right','color','red'); grid on; axis equal ax = axis; plot(ax(1:2),[0 0],'g',[0 0],ax(3:4),'g') % draw horizontal and vertical axes in green xlabel('c_1'); ylabel('c_3') hold off figure(2) % plot(c2,c3) plot(C(2,:),C(3,:),'o'); hold on text(C(2,:),C(3,:),athletenames,'FontSize',7,'VerticalAlignment','bottom'); z = zeros(1,n); plot([z;W(:,2)'],[z;W(:,3)'],'r'); % plot projected unit vectors for events text(W(:,2),W(:,3),eventnames,'FontSize',7,'VerticalAlignment','bottom','HorizontalAlignment','right','color','red'); grid on; axis equal ax = axis; plot(ax(1:2),[0 0],'g',[0 0],ax(3:4),'g') % draw horizontal and vertical axes in green xlabel('c_2'); ylabel('c_3') hold off
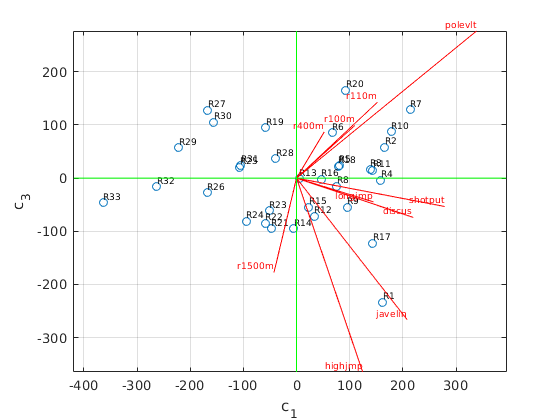
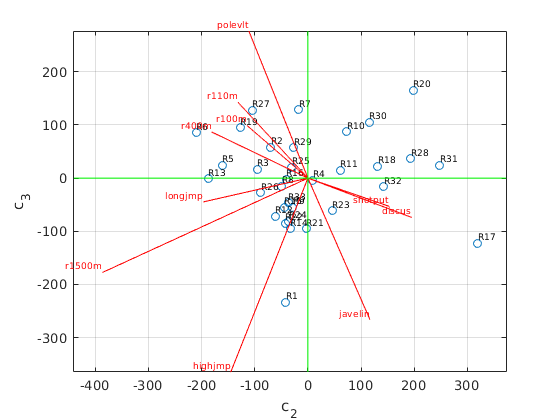
Interpretation of the result
We see that the third principal component c3 increases with running events and pole vault, and decreases most strongly with high jump, javelin, 1500m.