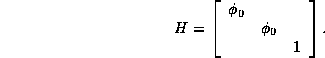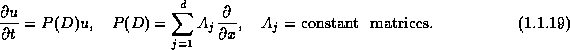
Define the Fourier symbol associated with P(D):
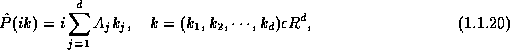
which arises naturally when we Fourier transform (hyper.18),
Solving the ODE (hyper.20) we find, as before, that hyperbolicity amounts to
For this to be true the necessary condition should hold, namely
We consider the ![]() -periodic constant coefficients system
-periodic constant coefficients system
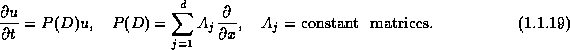
Define the Fourier symbol associated with P(D):
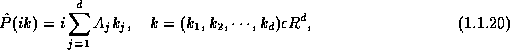
which arises naturally when we Fourier transform (hyper.18),
![]()
Solving the ODE (hyper.20) we find, as before, that hyperbolicity amounts
to
![]()
For this to be true the necessary condition
should hold, namely
![]()
: For the wave equation, (1.1.4),
![]() .
.
But the Gårding-Petrovski condition is not sufficient for the
hyperbolic estimate
(1.1.18) as told by the counterexample
![]()
As before, in this case we have ![]() , hence the
Gårding-Petrovski condition is fulfilled. Yet, Fourier
analysis shows that we need both
, hence the
Gårding-Petrovski condition is fulfilled. Yet, Fourier
analysis shows that we need both ![]() and
and
![]() in order to upperbound
in order to upperbound
![]() . Thus, the best we can hope for with this
counterexample is an a priori estimate of the form
. Thus, the best we can hope for with this
counterexample is an a priori estimate of the form
![]()
We note that in this case we have a "loss" of one derivative, and this
brings us to
the notion of
:
We say that the system (1.1.17) is weakly hyperbolic if there
exists an ![]() such that the following a priori estimate holds:
such that the following a priori estimate holds:
![]()
The Gårding-Petrovski condition is necessary and sufficient for the system
(hyper.18) to be weakly hyperbolic.
A necessary and sufficient characterization of hyperbolic systems is provided
by the
Kreiss matrix theorem: it states that (hyper.21) holds iff there exists a
positive
symmetrizer ![]() such that
such that
![]()
and this yields the conservation of the ![]() -weighted norm,
-weighted norm,
![]() ; that is,
; that is,
![]()
is conserved in time.
: For an a priori estimate forward in time (![]() ), it will suffice to have
), it will suffice to have
![]()
Indeed, we have in this case
![]()
and hence summing over all k's and using Parseval's equality
![]()
Two important subclasses of hyperbolic equations
are the strictly hyperbolic systems -- where
![]() has distinct real eigenvalues so that
has distinct real eigenvalues so that ![]() can be
real diagonalized
can be
real diagonalized
![]()
and as before, ![]() will do; the other
important case consists of symmetric hyperbolic systems
which can be
symmetrizer in the physical
space, i.e. there exists an H > 0 such that
will do; the other
important case consists of symmetric hyperbolic systems
which can be
symmetrizer in the physical
space, i.e. there exists an H > 0 such that
![]()
Most of the physically relevant systems fall into these categories.
: Shallow water equations (linearized)
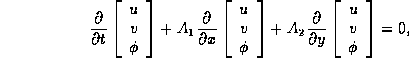
with
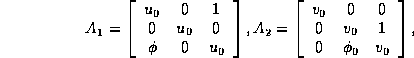
can be symmetrized with