isentropic equations
We consider the system of isentropic equations,
governing
the density 
and momentum 
,
Here 
is the pressure which is assumed to satisfy the
(scaled) 
law, 
.
The question of existence for this model, depending on the
-law, 
, was already studied
[7],[6] by compensated
compactness arguments.
Here we revisit this problem with the kinetic formulation
presented below which leads to existence result for
, consult [23], and is complemented with a
new existence proof for , consult [21].
For the derivation of our kinetic formulation of (2.5.36),
we start by seeking all weak entropy inequalities associated with
the isentropic system (2.5.36),
The family of entropy functions associated with (2.5.37)
consists of those 
's whose Hessians symmetrize the
Jacobian, A'(w); the requirement of a symmetric 
yields the Euler-Poisson-Darboux equation, e.g, [6]
Seeking weak entropy functions such that 
,
leads to the family of weak (entropy, entropy flux) pairs,
, depending on an arbitrary
,
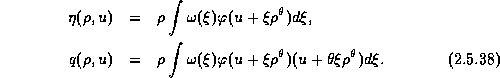
Here, 
is given by
We note that 
is convex iff is.
Thus by the formal change of variables,
,
the weight function becomes the
'pseudo-Maxwellian',
,
We arrive at the kinetic formulation of (2.5.36) which reads
Observe that integration of (2.5.40) against any
convex recovers all the weak entropy inequalities.
Again, as in the scalar case, the nonpositive measure m on the right of
(2.5.40), measures the loss of entropy which concentrates
along shock discontinuities.
The transport equation (2.5.40) is not purely kinetic
due to the dependence on the macroscopic velocity u
(unless 
corresponding to 
),
Compensated compactness arguments presented in [23] yield the following compactness result.
Finally, we consider the system
endowed with the pressure law
The system (2.5.41)-(2.5.42)
governs the isentropic gas dynamics
written in Lagrangian coordinates.
In general the equations (2.5.41)-(2.5.42) will be
referred to as the p-system (see [20],[30]).
For a kinetic formulation, we first seek the (entropy,entropy flux) pairs,
, associated with (2.5.41)-(2.5.42).
They are determined by the relations
where F is computed by the compatibility relations
The solutions of (2.5.43) can be expressed in terms
of the fundamental solution
where the fundamental solutions, 
, are given by
Here and below, 
(rather than v occupied
for the specific volume)
denotes the kinetic variable.
The corresponding kinetic fluxes are then given by
We arrive at the kinetic formulation of (2.5.41)-(2.5.42)
which reads, [23]
with macroscopic velocity, 
.
