We consider the convex conservation law
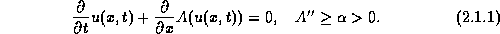
Starting with two values at the different positions,
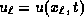and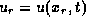 
, we trace these values by backward characteristics.
They impinge on the initial line at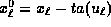 
and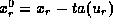 
, respectively.
Since the characteristics of entropy solutions of convex
conservation laws cannot intersect, one finds that
the ratio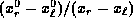 
remains positive for all time.
After rearrangement this yields
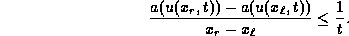
Thus we conclude that the velocity of a(u) satisfies the
Oleinik's one-sided Lip condition,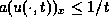 
.
Thanks to the convexity of A, we obtain the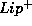 
bound on u itself,
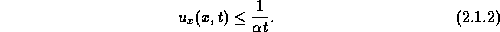
We recall that 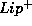bound (2.1.2) served as the cornerstone
for the Lip' convergence theory outlined in Lecture IV.
Here we focus on the issue of it regularity.
Granted (2.1.2), it follows that
the solution operator associated with convex conservation laws, 
,
has a nonlinear regularizing effect, mapping
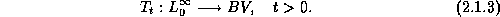
Indeed, for uniformly bounded initial data,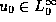 
, with
compact support of size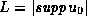 
, one obtains
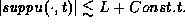The 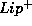bound
(2.1.2) then yields an upper bound on the positive variation,
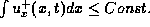; since the sum of the positive and negative
variations is bounded,
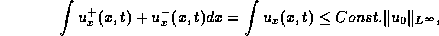
it follows that their difference is also bounded,
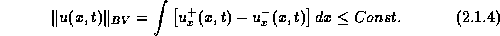
Observe that no regularity is 'gained' in the linear case,
where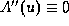 
.
Indeed, the compactness asserted in (2.1.3) is a purely
nonlinear regularizing phenomenon which reflects the
irreversibility of nonlinear conservation laws, due
to loss of entropy (information) across shock discontinuities.
Here, nonlinearity is quantified in terms
of convexity; in the prototype example of the inviscid Burgers'
equation,
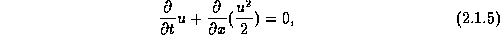
one finds a time decay,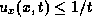 
.
Tartar [31] proved this regularizing effect for
general nonlinear fluxes -- nonlinear in the sense of
.
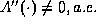The situation with multidimensional equations, however,
is less clear.
Consider the 'two-dimensional Burgers' equation',
analogous to (2.1.5)
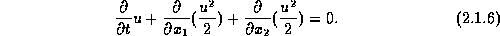
Since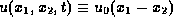 
is a steady solution of
(2.1.6) for any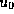 
, it follows
that initial oscillations persist (along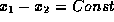 
),
and hence there is no regularizing effect which guarantee
the compactness of the solution operator in this case.
More on oscillations and discontinuities can be found in Tartar's
review [32].