)
We deal with solutions to transport equations
The averaging lemmas, [13], [12], [11],
state that in
the generic non-degenerate case, averaging over the velocity space, 
, yields a gain of spatial regularity.
The prototype statement reads
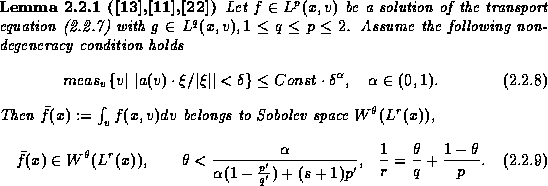
Variants of the averaging lemmas were used by DiPerna and Lions to
construct global weak (renormalized) solutions of Boltzmann,
Vlasov-Maxwell and related
kinetic systems, [9], [10]; in Bardos et. al.,
[1],
averaging lemmas were used to construct solutions of the incompressible
Navier-Stokes equations. We turn our attention to
their use in the context of
nonlinear conservation laws and related equations.
Proof.(Sketch). We shall sketch the proof in the
particular case, p=q which will suffice to demonstrate the
general 
case.
Let 
denote the set where the symbol 
is 'small',
and decompose the average, 
accordingly:
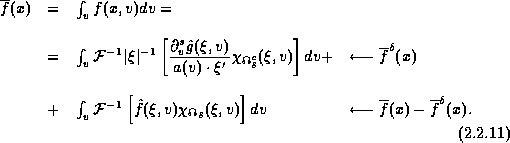
Here, 
represents the usual smooth partitioning
relative to 
and its complement, 
.
On 
, the symbol is 'bounded away' from zero, so we gain
one derivative:
On 
- along the `non uniformly elliptic' rays,
we have no gain of regularity, but instead, our non-degeneracy
assumption implies that 
is a 'small' set and therefore
Both (2.2.12) and (2.2.13)
are straightforward for p=2 and by estimating the
corresponding 
multipliers, the case 
follows
by interpolation.
Finally, we consider the K-functional
The behavior of this functional, 
,
characterize the smoothness of 
in the intermediate
space between 
and 
: more precisely,
belongs to Besov space 
with 'intermediate' smoothness of order 
.
Now set 
, then
with appropriately scaled 
we find
that with
. This means that 
belongs to Besov space,
and (2.2.9) (with p=q=r) follows. 
Remark.
In the limiting case of 
in (2.2.8),
one finds that if
then averaging is a compact mapping,
.
The case p=2 follows from Gèrard's results [12].