)In this section we resume our discussion on the regularization effect of nonlinear conservation laws. The averaging lemma enables us to identify the proper notion of 'nonlinearity' in the multivariate case, which guarantee compactness.
The following result, adapted from [22], is in the heart of matter.
Remark. Note that the bounded measure of entropy production in (2.3.17) need not be negative; general bounded measures will do.
Proof.To simplify notations, we use the customary
index for time direction,
The entropy condition (2.3.17) with Kruzkov entropy pairs
(
), reads
This defines a family of non-negative measures, 
,
Differentiate (2.3.18) w.r.t. v: one finds that the indicator
function, 
, where
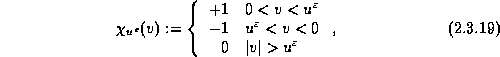
satisfies the transport equation,
which corresponds to (2.2.7) with
.
We now apply the averaging lemma with (s = q= 1, p = 2), which
tells us that 
as asserted. 
It follows that if the non-degeneracy condition (2.3.16) holds,
then the family of approximate solutions
is
compact and strong convergence follows.
In this context we refer to the
convergence statement for
measure-valued solutions for general multidimensional scalar conservation laws
- approximate solutions measured by their nonpositive entropy production
outlined in Lecture I, §.
Here, Theorem 2.3.1 yields even more, by
quantifying the regularity of
approximate solutions with bounded entropy productions in terms of the
non-degeneracy condition (2.3.16).
In fact, more can be said if the solution operator associated with
is
translation invariant: a bootstrap argument yields an
improved regularity, [22],
In particular, if the problem is nonlinear in the sense that
the non-degeneracy condition (2.2.14) holds,
then the corresponding
solution operator, 
, has a regularization effect mapping
.
This could be viewed as a multidimensional generalization for
Tartar's regularization result for a.e. nonlinear one-dimensional
fluxes, 
.
We continue with few multidimensional examples which illustrate the relation between the non-degeneracy condition, (2.3.16) and regularity.
Example #1. The 'two-dimensional Burgers' equation'
(2.1.6),
has a linearized symbol 
which fails to satisfy
the non-degeneracy/non-linearity condition (2.3.16),
since it vanishes 
's
along 
. This corresponds to its persistence of
oscillations along 
, which excludes compactness.
In this case the linearized symbol is given by
; Here we have
(just consider the second-order touch-point at v=1).
Hence, the solution operator associated with (2.3.23) is compact
( - in fact, mapping 
.)
Example #3. Consider
For 
we obtain an index of non-degeneracy/non-linearity
of order 
.
