Theorem 2.3.1
provides an alternative route to analyze the convergence of
general entropy stable multi-dimensional
schemes, schemes whose convergence proof was previously accomplished by
measure-valued arguments; here we refer to finite-difference,
finite-volume, streamline-diffusion and spectral approximations ...,
which were studied in
[4, 18, 19, 15, 16, 3].
Indeed, the feature in the convergence proof of all these methods is the
-compact entropy
production, (2.4.33). Hence,
if the underlying conservation law satisfies
the non-linear degeneracy condition (2.3.22),
then the corresponding family of approximate solutions,
becomes compact. Moreover, if the entropy production is bounded measure,
then there is actually a gain of regularity indicated in
Theorem 2.3.1 and respectively,
in (2.3.21) for the translation invariant case.
Remark.
Note that unlike the requirement for a nonpositive
entropy production from measure-valued solutions
(consult (
) in Lecture I), here we allow for an arbitrary
bounded measure.
So far we have not addressed explicitly a kinetic formulation of the multidimensional conservation law (2.3.15). The study of regularizing effect for multidimensional conservation laws was originally carried out in [22] for the approximate solution constructed by the following BGK-like model, [28] (see also [2],[14]),
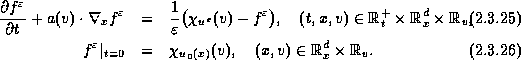
Here, 
denotes the
`pseudo-Maxwellian',
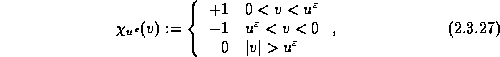
which is associated with the average of 
,
The key property of this kinetic approximation is the existence
of a nonnegative measure, 
such that
(The existence of such measures proved in [22]
and is related to H-functions studied in [28] and
Brenier's lemma [2].)
Thus, we may rewrite (2.3.25) in the form
Let 
be an entropy pair associated with (2.3.15).
Integration of (2.3.29) against 
implies that the
corresponding macroscopic averages,
, satisfy
Thus, the entropy production in this case is nonpositive and hence a bounded
measure, so that Theorem 2.3.1 applies.
Viewed as a measure-valued solution, convergence follows along
DiPerna's theory [8]. If, moreover, the
nondegeneracy condition (2.3.16) holds, then we can further
quantify the 
-regularity (of order 
.)
Theorem 2.3.1 offers a further generalization beyond the original, 'kineticly' motivated discussion in [22]. Indeed, consideration of Theorem 2.3.1 reveals the intimate connection between the macroscopic assumption of bounded entropy production in (2.3.17), and an underlying kinetic formulation ({2.3.20), analogous to (2.3.29). For a recent application of the regularizing effect for a convergence study of finite-volume schemes along these lines we refer to [24].