Upwind schemes

Let abbreviates the cell averages, . By sampling (1.2.4) at the mid-cells, , we obtain an evolution scheme for these averages, which reads
 
Here, it remains to recover the pointvalues, , in terms of their known cell averages, , and to this end we proceed in two steps:

• First, the reconstruction - we recover the pointwise values of at , by a reconstruction of a piecewise polynomial approximation
   
  
• Second, the evolution -- are determined as the solutions of the generalized Riemann problems
   
  

The solution of (1.2.7) is composed of a family of nonlinear waves - left-going and right-going waves. An exact Riemann solver, or at least an approximate one is used to distribute these nonlinear waves between the two neighboring cells, and . It is this distribution of waves according to their direction which is responsible for upwind differencing, consult Figure 1.2.1. We briefly recall few canonical examples for this category of upwind Godunov-type schemes.

  
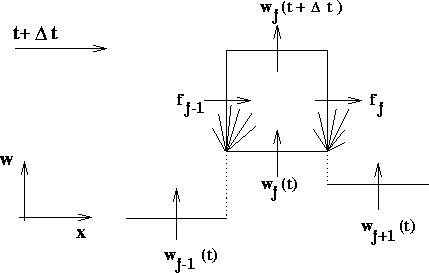
Figure 1.2.1: Upwind differencing by Godunov-type scheme.

The original Godunov scheme is based on piecewise-constant reconstruction, , followed by an exact Riemann solver. This results in a first-order accurate upwind method [11], which is the forerunner for all other Godunov-type schemes. A second-order extension was introduced by van Leer [19]: his MUSCL scheme reconstructs a piecewise linear approximation, , with linear pieces of the form so that . Here the -s are possibly limited slopes which are reconstructed from the known cell-averages, . (Throughout this lecture we use primes, , to denote discrete derivatives, which approximate the corresponding differential ones). A whole library of limiters is available in this context, so that the co-monotonicity of with is guaranteed, e.g., [42]. The Piecewise-Parabolic Method (PPM) of Colella-Woodward [6] and respectively, ENO schemes of Harten et.al. [13], offer, respectively, third- and higher-order Godunov-type upwind schemes. (A detailed account of ENO schemes can be found in lectures of C.W. Shu in this volume). Finally, we should not give the impression that limiters are used exclusively in conjunction with Godunov-type schemes. The positive schemes of Liu and Lax, [27], offer simple and fast upwind schemes for multidimensional systems, based on an alternative positivity principle.