Central schemes

As before, we seek a piecewise-polynomial, , which serves as an approximate solution to the exact evolution of sliding averages in (1.2.4),
 

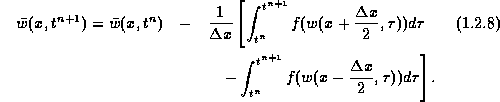
Note that the polynomial pieces of are supported in the cells, , with interfacing breakpoints at the half-integers gridpoints, .

We recall that upwind schemes (1.2.5) were based on sampling (1.2.4) in the midcells, . In contrast, central schemes are based on sampling (1.2.8) at the interfacing breakpoints, , which yields
 
We want to utilize (1.2.9) in terms of the known cell averages at time level . The remaining task is therefore to recover the pointvalues , and in particular, the staggered averages, . As before, this task is accomplished in two main steps:

• First, we use the given cell averages , to reconstruct the pointvalues of as piecewise polynomial approximation
   
  In particular, the staggered averages on the right of (1.2.9) are given by
   
  The resulting central scheme (1.2.9) then reads
   
  
• Second, we follow the evolution of the pointvalues along the mid-cells, , which are governed by
   
  Let denote the eigenvalues of the Jacobian . By hyperbolicity, information regarding the interfacing discontinuities at
  propagates no faster than . Hence, the mid-cells values governed by (1.2.13), , remain free of discontinuities, at least for sufficiently small time step dictated by the CFL condition . Consequently, since the numerical fluxes on the right of (1.2.12), , involve only smooth integrands, they can be computed within any degree of desired accuracy by an appropriate quadrature rule.

  
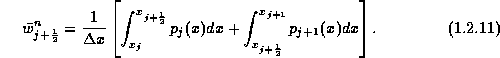
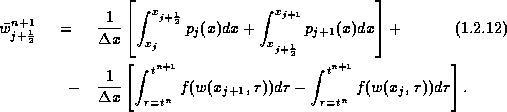
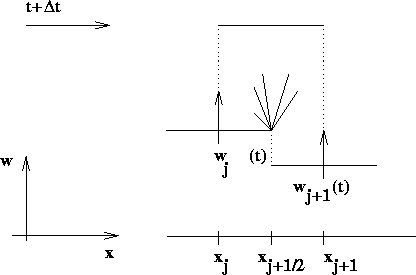
Figure 1.2.2: Central differencing by Godunov-type scheme.

It is the staggered averaging over the fan of left-going and right-going waves centered at the half-integered interfaces, , which characterizes the central differencing, consult Figure 1.2.2. A main feature of these central schemes - in contrast to upwind ones, is the computation of smooth numerical fluxes along the mid-cells, , which avoids the costly (approximate) Riemann solvers. A couple of examples of central Godunov-type schemes is in order.

The first-order Lax-Friedrichs (LxF) approximation is the forerunner for such central schemes -- it is based on piecewise constant reconstruction, with . The resulting central scheme, (1.2.12), then reads (with the usual fixed mesh ratio )
 
Our main focus in the rest of this chapter is on non-oscillatory higher-order extensions of the LxF schemes.