Following the framework outlined in §1.3.1, the upgrade to third-order central scheme consists of two main ingredients:
Following [29], we proceed as follows.
The piecewise-parabolic reconstruction takes the form
Here, 
are the (pointvalues of) the reconstructed second
derivatives
are the (pointvalues of) the reconstructed slopes,
and 
are the reconstructed pointvalues
Observe that, starting with third- (and higher-) order accurate methods,
pointwise values cannot be interchanged with cell averages,
.
Here, 
are appropriate nonlinear limiters which guarantee
the non-oscillatory behavior of the third-order reconstruction;
its precise form can be found in [28],
[29].
They guarantee that the reconstruction (1.3.20) is non-oscillatory
in the sense
that 
-- the number of extrema of
, does not exceed that of its piecewise-constant projection,
,
Next we turn to the evolution of the piecewise-parabolic
reconstructed solution.
To this end we need to evaluate the staggered averages,
, and to approximate the interface fluxes,
.
With 
specified in
(1.3.20)-(1.3.23), one evaluates the staggered averages of the third
order reconstruction 
Remarkably, we obtain here the same formula for the staggered averages as in
the second-order cases, consult (1.3.17); the only difference is the use of
the new limited slopes in (1.3.22), 
.
Next, we approximate the (exact) numerical fluxes by Simpson's quadrature
rule, which is (more than) sufficient for retaining the overall third-order
accuracy,
This in turn, requires the three approximate pointvalues on the
right, 
for 
. Following our approach in the second-order case,
[31],
we use Taylor expansion to predict
In summary of the scalar setup, we end up with a two step scheme where,
starting with the reconstructed pointvalues
we predict the pointvalues 
by, e.g. Taylor
expansions,
this is followed by the corrector step
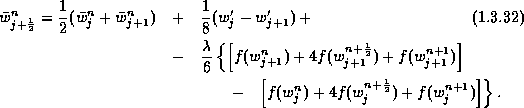
In figure 1.3.2 we revisit the so called Woodward-Colella problem, [46], where we compare the second vs. the third-order results. The improvement in resolving the density field is evident.
We conclude this section with several remarks. Remarks.
We briefly mention the stability results for the scalar central schemes. In the second order case, the NT scheme was shown to be both TVD and entropy stable in the sense of satisfying a cell entropy inequality - consult [31]. The third-order scalar central scheme is stable in the sense of satisfying the NED property, (1.3.24), namely
Extensions of the central framework which deal with both, stiff and non-stiff source terms can be found in [37],[38], [8], [4]. In particular, Kupferman in [20],[21] developed the central framework within the radial coordinates which require to handle both - variable coefficients + source terms.
We refer to [39], where a high-order ENO reconstruction is realized by a staggered cell averaging. Here, intricate Riemann solvers are replaced by high order quadrature rules. and for this purpose, one can effectively use the RK method (rather than the Taylor expansion outlined above):
The evaluations of Taylor expansions could be substituted by the more economical Runge-Kutta integrations; the simplicity becomes more pronounced with systems. A particular useful approach in this context was proposed in [39], using the natural continuous extensions of RK schemes.
One of the main advantages of our central-staggered framework over that of
the upwind schemes, is that expensive and time-consuming characteristic
decompositions can be avoided.
Specifically, all the non-oscillatory
computations can be carried out with diagonal limiters,
based on a
component-wise extension of the scalar
limiters outlined above.
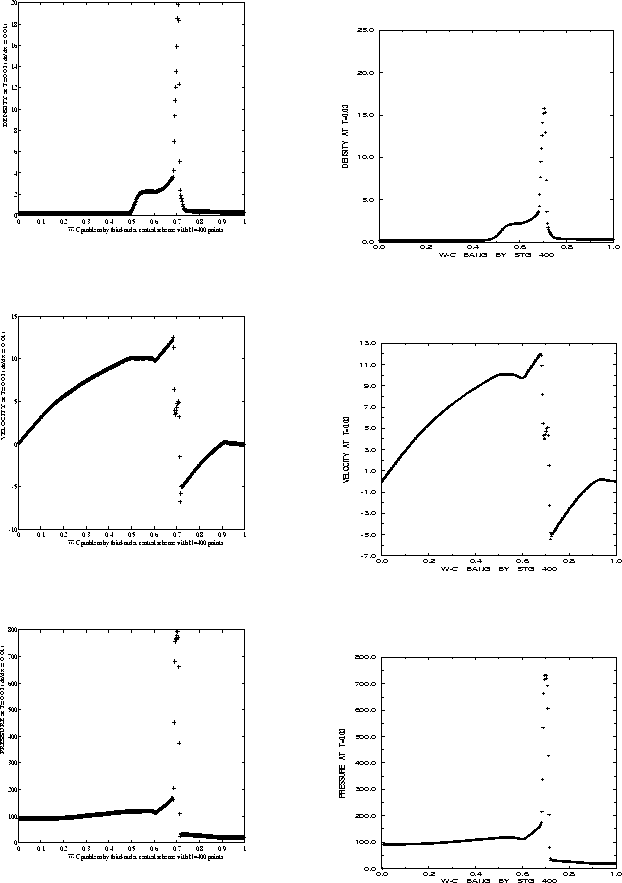
Figure 1.3.5: 
vs. 
order central schemes --
Woodward-Colella problem
at t=0.03
