, based on linear functions 
which
are supported at
the cells 
(see Figure 1.3.3),
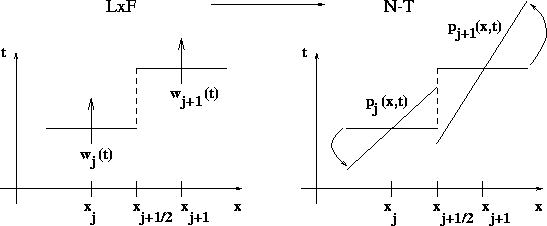
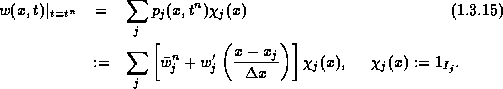
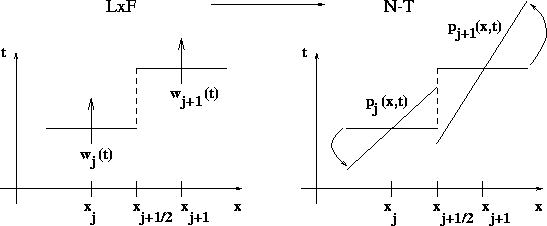
Figure 1.3.3: The second-order reconstruction
Second-order of accuracy is guaranteed if the
discrete slopes approximate the corresponding derivatives,
.
Such a non-oscillatory approximation of the derivatives is possible, e.g., by using
built-in non-linear limiters of the form
Here and below, 
is a non-oscillatory limiter and MM denotes the Min-Mod
function
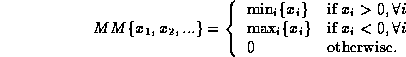
An exact evolution of w, based on integration of the conservation law over the
staggered cell, 
, then reads, (1.2.9)
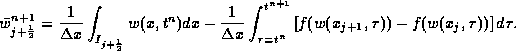
The first integral is the staggered cell-average at time 
, 
,
which can be computed directly from the above reconstruction,
The time integrals of the flux are computed by the second-order accurate
mid-point quadrature rule
Here, the Taylor expansion is being used to predict the required
mid-values of w
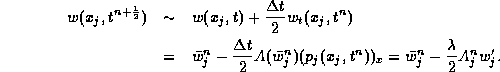
In summary, we end up with the central scheme,
[31], which consists of a
first-order predictor step,
followed by the second-order corrector step, (1.2.12),
The scalar non-oscillatory properties of (1.3.18)-(1.3.19)
were proved in [31],
[32], including the TVD property, cell entropy inequality,
error estimates, etc.
Moreover, the numerical experiments, reported in
[30], [31], [2],
[3], [45], [37],
[38], [39],
with one-dimensional systems
of conservation laws, show that such second-order central schemes enjoy the same
high-resolution as the corresponding second-order upwind schemes do.
Thus, the excessive smearing typical to the first-order LxF central scheme
is compensated here by the second-order accurate MUSCL reconstruction.
In figure 1.3.4 we compare, side by side, the upwind ULT scheme of Harten, [12], with our central scheme (1.3.18)-(1.3.19). The comparable high-resolution of this so called Lax's Riemann problem is evident.
At the same time, the central scheme (1.3.18)-(1.3.19) has the advantage over the corresponding upwind schemes, in that no (approximate) Riemann solvers, as in (1.2.7), are required. Hence, these Riemann-free central schemes provide an efficient high-resolution alternative in the one-dimensional case, and a particularly advantageous framework for multidimensional computations, e.g., [3], [2], [16]. This advantage in the multidimensional case will be explored in the next section. Also, staggered central differencing, along the lines of the Riemann-free Nessyahu-Tadmor scheme (1.3.18)-(1.3.19), admits simple efficient extensions in the presence of general source terms, [8], and in particular, stiff source terms, [4]. Indeed, it is a key ingredient behind the relaxation schemes studied in [18].
It should be noted, however, that the component-wise version
of these central schemes might result in deterioration of resolution
at the computed extrema. The second-order computation
presented in figure 1.3.2 below demonstrates this point.
(this will be corrected by higher order central methods).
Of course, this - so called extrema clipping, is
typical to high-resolution upwind schemes as well;
but it is more pronounced with our central schemes due to the built-in
extrema-switching to the dissipative LxF scheme. Indeed,
once an extrema cell, , is detected (by the limiter), it sets a zero
slope, 
, in which case the second-order scheme
(1.3.18)-(1.3.19) is reduced back to the first-order LxF, (1.2.14).
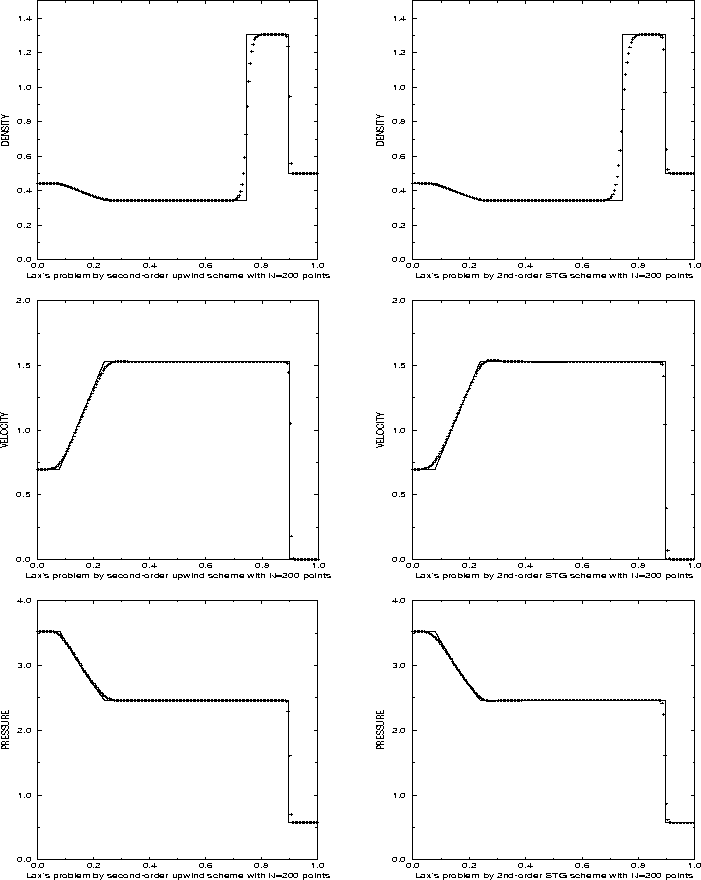
Figure 1.3.4: 2nd order: central (STG) vs.
upwind (ULT) -- Lax's Riemann problem