To approximate a solution to (1.4.34), we start with a two-dimensional linear reconstruction
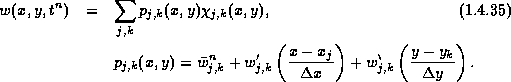
Here, the discrete slopes in the x and in the y direction approximate the corresponding derivatives,
-1
Following the one dimensional setup, one can derive a non-oscillatory, two-dimensional central scheme. Here we sketch the construction of the second-order two-dimensional scheme following [16] (see also [2],[1]). For the two-dimensional third-order accurate scheme, we refer to [24].
We consider the two-dimensional hyperbolic system of conservation laws
![]()
To approximate a solution to (1.4.34), we start with a two-dimensional
linear reconstruction
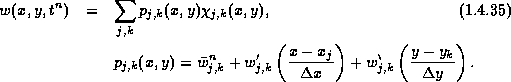
Here, the discrete slopes in the x and in the y direction approximate the
corresponding derivatives,
![]() , and
, and
![]() is the characteristic function of the cell
is the characteristic function of the cell
![]() .
Of course, it
is essential to reconstruct the discrete slopes,
.
Of course, it
is essential to reconstruct the discrete slopes, ![]() and
and ![]() ,
with built in limiters, which guarantee the non-oscillatory
character of the reconstruction;
the family of min-mod limiters is a prototype example
,
with built in limiters, which guarantee the non-oscillatory
character of the reconstruction;
the family of min-mod limiters is a prototype example
![]()
![]()
![]()
-1![]()
![]()
![]()
An exact evolution of this reconstruction, which is based on integration of the conservation law over the staggered volume yields
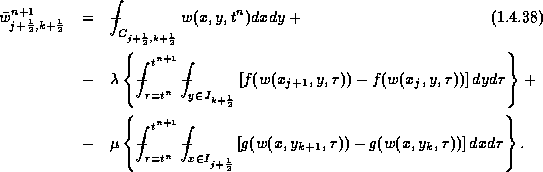
The exact averages at ![]() - consult the floor plan in Figure
1.4.6 yields
- consult the floor plan in Figure
1.4.6 yields
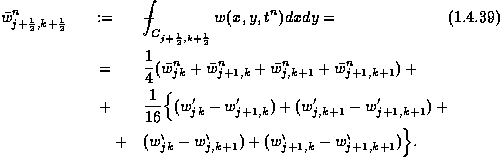
So far everything is exact.
We now turn to approximate the four fluxes on the right of
(1.4.37),
starting with the one along the East face, consult figure 1.4.7,
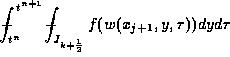 .
We use the midpoint quadrature rule for second-order approximation of the
temporal integral,
.
We use the midpoint quadrature rule for second-order approximation of the
temporal integral, ![]() ; and, for reasons to be clarified below, we use the second-order
rectangular quadrature rule for the spatial integration across the y-axis,
yielding
; and, for reasons to be clarified below, we use the second-order
rectangular quadrature rule for the spatial integration across the y-axis,
yielding
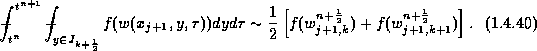
In a similar manner we approximate the remaining fluxes.
These approximate fluxes make use of
the midpoint values,
![]() ,
and it is here that we take advantage of utilizing these midvalues for
the spatial integration by the rectangular rule. Namely, since these
midvalues are secured at the smooth center of their cells,
,
and it is here that we take advantage of utilizing these midvalues for
the spatial integration by the rectangular rule. Namely, since these
midvalues are secured at the smooth center of their cells, ![]() ,
bounded away from the jump discontinuities along the edges, we may use
Taylor expansion,
,
bounded away from the jump discontinuities along the edges, we may use
Taylor expansion, ![]() . Finally,
we use the conservation law (1.4.34) to express the time
derivative,
. Finally,
we use the conservation law (1.4.34) to express the time
derivative, ![]() , in terms of the spatial derivatives,
, in terms of the spatial derivatives, ![]() and
and ![]() ,
,
![]()
Here, ![]() and
and
![]() , are one-dimensional
discrete slopes in the x- and y-directions, of the type reconstructed
in (1.4.36)-(1.4.36); for example,
multiplication
by the corresponding Jacobians A and B yields
, are one-dimensional
discrete slopes in the x- and y-directions, of the type reconstructed
in (1.4.36)-(1.4.36); for example,
multiplication
by the corresponding Jacobians A and B yields
![]()
Equipped with the midvalues (1.4.40), we can now evaluate the
approximate fluxes, e,g., (1.4.39). Inserting these
values, together with the staggered average computed in
(1.4.39), into (1.4.37), we conclude with new staggered
averages at ![]() , given by
, given by
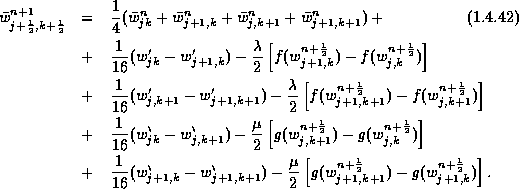
In summary, we end up with a simple two-step predictor-corrector scheme
which could be conveniently expressed in terms on the
one-dimensional staggered averaging notations
![]()
Our scheme consists of a predictor step
![]()
followed by the corrector step
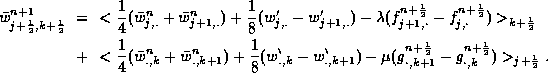
In figures 1.4.8 taken from [16], we present the two-dimensional computation of a double-Mach reflection problem; in figure 1.4.9 we quote from [45] the two-dimensional computation of MHD solution of Kelvin-Helmholtz instability due to shear flow. The computations are based on our second-order central scheme. It is remarkable that such a simple 'two-lines' algorithm, with no characteristic decompositions and no dimensional splitting, approximates the rather complicated double Mach reflection problem with such high resolution. Couple of remarks are in order.
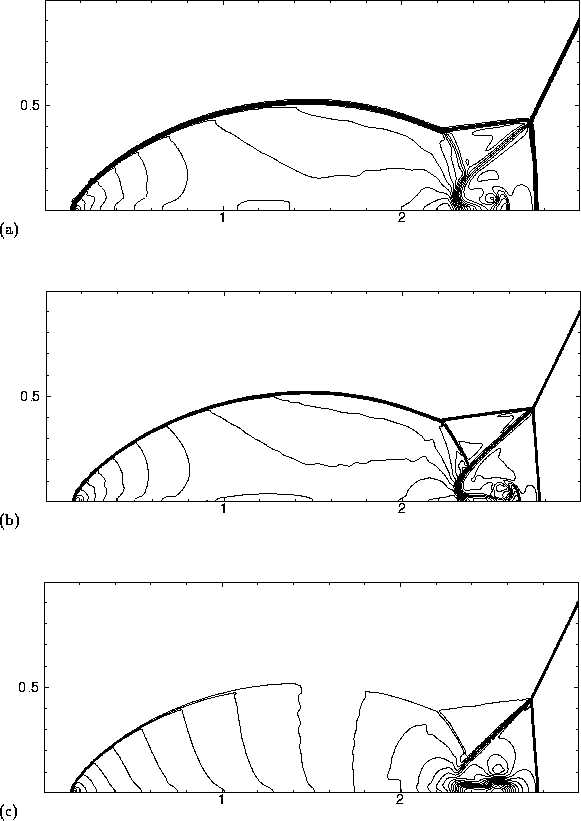
Figure 1.4.8: Double Mach reflection problem computed with the
central scheme using ![]() limiter with
CFL=0.475 at t=0.2
(a) density computed with
limiter with
CFL=0.475 at t=0.2
(a) density computed with ![]() cells
(b) density computed with
cells
(b) density computed with ![]() cells
(c) x-velocity computed with
cells
(c) x-velocity computed with ![]() cells
cells
We conclude this section with brief remarks on further results related to central schemes. Remarks.
Again, we would like to highlight the simplicity of the central schemes, which is particularly evident in the multidimensional setup: no characteristic information is required - in fact, even the exact Jacobians of the fluxes are not required; also, since no (approximate) Riemann solvers are involved, the central schemes require no dimensional splitting; as an example we refer to the approximation of the incompressible equations by central schemes, §1.5; the results in [7] provide another example of a weakly hyperbolic multidimensional system which could be efficiently solved in term of central schemes, by avoiding dimensional splitting.
The following maximum principle holds for the nonoscillatory scalar central schemes: