Crystal surface morphological evolution below the roughening temperature:
From microscopic models to macroscopic limits (and back)
Small structures and devices, with sizes ranging from the
order of nanometer (1 nm = 1/100,000 of human hair thickness) up to a few microns,
have properties that may revolutionize modern communications and information technology. The design and fabrication of such
devices requires a precise control over their morphological evolution, especially their decay. When the dominant
mechanism of mass transport is surface diffusion, as it happens in many situations of experimental interest,
the lifetime of small surface features scales
as a large power (usually fourth) of their size and typically varies as an Arrhenius function
of temperature. (Hence, the lifetime increases with decreasing temperature).
It follows that fabricating smaller and smaller devices would imply
using lower and lower temperatures.
Above the roughening transition temperature, crystal surfaces can be treated
as smooth, and their morphological evolution is well understood via the pioneering works of Mullins,
Herring and others in the 1950s and 1960s. By contrast, below the roughening transition
temperature, crystal surfaces develop distinct atomic steps separated by nanoscale
terraces, may have facets (macroscopic planar regions), and thus cannot be treated always
as smooth. The study of crystal surface morphological evolution below the roughening transition is
an area of active research, posing numerous analytical challenges.
My research focuses on the quantitative description of crystal morphological
evolution
below roughening.
A theme that I have been exploring
is the
use and limitations of macroscopic
theories and equations, such as PDEs, based on
the fundamentals of step motion, and even on models at smaller scales when possible.
I am especially interested in
microscale effects that leave their signatures in the
macroscopic limit.
For example, a basic problem
is how to solve the requisite 4th-order, nonlinear parabolic PDEs on sloping surfaces by
finding and applying suitable boundary conditions at edges of facets, which
are "free boundaries" for such PDEs. These boundary conditions
in principle
involve microscale features of the motion of individual steps on top of facets yet do affect surface
profiles macroscopically.
Solutions to the related
PDEs develop singularities at these moving boundaries.
Addressing these issues
requires study of coupled differential equations for the step positions,
first for simple morphologies of steps that are everywhere parallel, and then for
more general cases in two independent space dimensions. The central issue is how
to link solutions to the coupled ODE system with the PDE solution near the facet edge.
Most recently, I have been interested in quantum effects, especially electronic surface state effects, on the
macroscopic
free energy of crystal surfaces.
Disclaimer: The article files provided here are intended for the convenience of the reader and for personal use only.
Personal use of this material means that it is not permitted to upload it to any public server, on-line service, network, or bulletin board; make copies for any commercial purpose;
retransmit or redistribute it without written permissions from the paper's publisher and author.
Reproduction or storage of material retrieved from this site is subject to the U.S. Copyright Act of 1976, Title 17 U.S.C.
Research leading to some of the publications listed on this page was
supported by the National Science Foundation through grants: DMS-1412769 (2015-18),
DMS-0847587 (2009-14)
and DMR-0520471 (2007-09).
Topics and papers:
I.
Numerical simulation by the finite-element method
of PDE
for crystal surface morphological
relaxation in 2+1
dimensions with periodic
boundary conditions. We numerically observe sharp topographic
transitions from 2D to almost 1D profiles.
Collaborators: A. Bonito, R. H. Nochetto. Grad. student: J. Quah.
Numerical experiments: Surface height profile:
Initial aspect ratio 3:2;
zero
line tension (no facets).
Anisotropic PDE (Margetis-Kohn theory; see publication II.1 below):
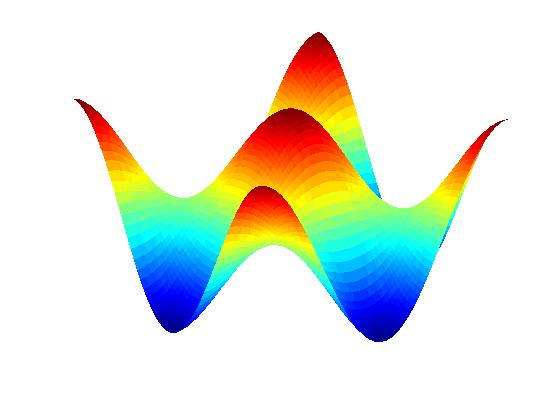
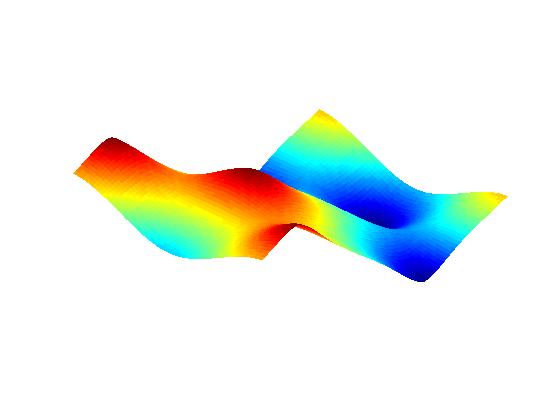
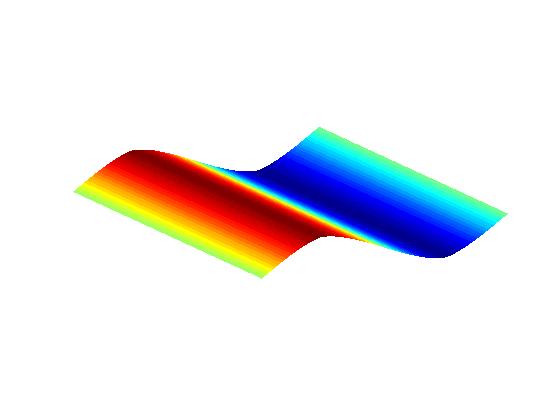
(Time flows from left to right)
Simulations from previous isotropic theory
(e.g., Shenoy et al., Phys. Rev. Lett. Vol. 92, art. 256101 (2004), and also publication V.2 below)
for comparison purposes:
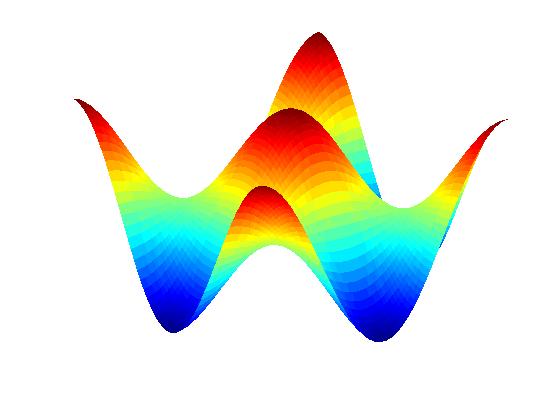
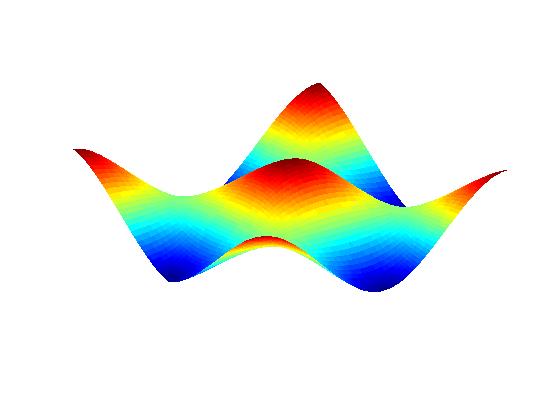
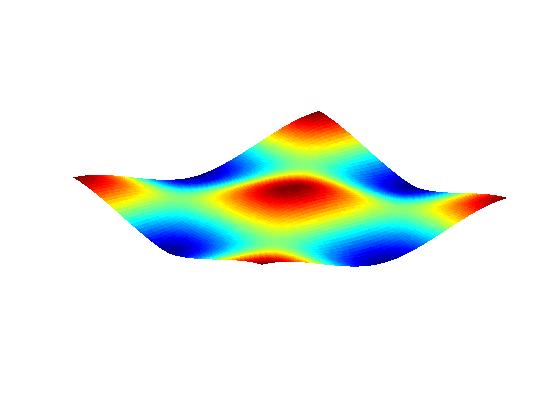
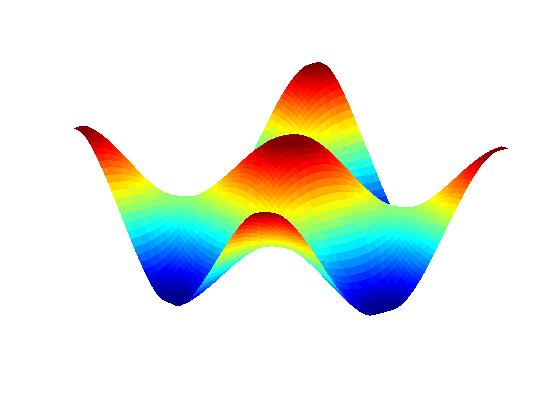
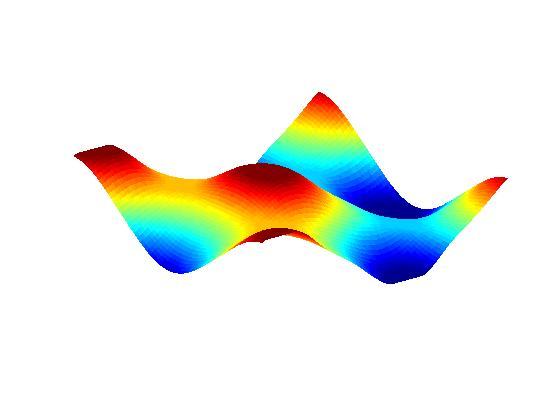
Anisotropic PDE theory with
``small'' line tension (facets form):
The FEM results here do NOT account for microscale effects on top of facets.
(For the radial case, see publication V.1 below.)

Papers:
1. Bonito, A., R. H. Nochetto, J. Quah, and D. Margetis (2009),
``Self-organization of decaying surface corrugations:
A numerical study'',
Physical Review E, Vol. 79, 050601(R), 4pp.
II.
Derivation of macroscopic PDE for
crystal surface morphological relaxation from
step motion (BCF-type models)
in 2+1 dimensions:
Anisotropy of macroscopic surface flux;
plausible unified treatment of observed, different decay laws for
height profile in periodic settings of
Si(001) and Ag(110).
1. D. Margetis and R. V. Kohn (2006),
Continuum relaxation of interacting steps on crystal surfaces in (2+1) dimensions
(PDF),
(SIAM Journal on) Multiscale Modeling & Simulation, Vol. 5, pp. 729-758.
2. D. Margetis (2007),
Unified continuum approach to crystal surface
morphological relaxation
(PDF), Physical Review B, Vol. 76, art. 193403, 4pp.
Extensions:
3. J. Quah and D. Margetis (2008),
Anisotropic diffusion in continuum relaxation of stepped
crystal surfaces (PDF),
Journal of Physics A: Mathematical & Theoretical, Vol. 41, art. 235004, 18pp.
4. J. Quah, J. Young, and D. Margetis (2008),
Macroscopic view of crystal-step
transparency,
Physical Review E, Vol. 78, 042602, 4pp.
5. D. Margetis (2009),
Homogenization of reconstructed crystal surfaces: Fick's law of diffusion,
Physical Review E, Vol. 79, 052601, 4pp.
6. J. Quah and D. Margetis (2010),
Electromigration in macroscopic relaxation of stepped surfaces,
(SIAM) Multiscale Modeling & Simulation, Vol. 8, pp. 667-700.
7. D. Margetis and K. Nakamura (2012),
Homogenization of composite vicinal surfaces: Evolution laws in 1+1 dimensions,
Physica D, Vol. 241, pp. 1179-1189.
8. K. Nakamura
and D. Margetis (2013),
Phase field model for reconstructed
stepped surface
,
Physical Review E, Vol. 88, art. 014401 (4pp).
III.
Derivation of macroscopic/mesoscopic PDE for material deposition
on stepped crystal surfaces in 2+1 dimensions.
Related paper:
1. D. Margetis (2010),
A stochastic step flow model with growth in 1+1 dimensions,
Journal of Physics A: Mathematical & Theoretical, Vol. 43, art. 065003, 22pp.
2. P. Patrone, R. Wang, and D. Margetis (2011),
Small fluctuations in epitaxial growth via conservative noise,
Journal of Physics A: Mathematical and Theoretical, Vol. 44, art. 315002, 22pp.
IV.
Kinetic theory approach to studying
relation of models across scales, from atomistic to continuum;
use of kinetic (BBGKY) hierarchies for step correlations in deterministic
or stochastic settings in relaxation or growth.
Related papers:
1. D. Margetis and A. E. Tzavaras (2009),
Kinetic hierarchies and macroscopic limits for crystalline
steps in 1+1 dimensions,
(SIAM) Multiscale Modeling & Simulation,
Vol. 7, pp. 1428-1454.
2. D. Margetis (2010),
A stochastic step flow model with growth in 1+1 dimensions,
Journal of Physics A: Mathematical & Theoretical, Vol. 43, art. 065003, 22pp.
3. P. Patrone, T. L. Einstein, and D. Margetis (2010),
One-dimensional model of interacting-step fluctuations on vicinal surfaces:
Analytical formulas and kinetic Monte-Carlo simulations,
Physical Review E, Vol. 82, art. 061601, 18pp.
4. P. Patrone, R. Wang, and D. Margetis (2011),
Small fluctuations in epitaxial growth via
conservative noise,
Journal of Physics A: Mathematical and Theoretical,
Vol. 44, art. 315002, 22pp.
5. D. Margetis, P. N. Patrone, and T. L. Einstein (2011),
Stochastic models of epitaxial growth,
2010 Materials Research Society (MRS) Fall Meeting Proceedings, Vol. 1318, pp. UU7.4.1-UU7.4.6
(mrsf10-1318-uu07-04); DOI:10.1557/opl.2011.269.
6. P. Patrone
and D. Margetis (2014),
Connection of kinetic Monte Carlo model for surfaces to one-step flow
theory in 1+1 dimensions,
(SIAM) Multiscale Modeling Simulation, Vol. 12, pp. 364-395.
7. P. N. Patrone, T. L. Einstein, and
D. Margetis (2014),
From atoms to steps: the microscopic origins of crystal evolution,
Surface Science, Vol. 625, pp. 37-43.
8. J.-G. Liu, J. Lu, and D. Margetis (2015),
Emergence of step flow from an atomistic scheme of epitaxial growth in 1+1 dimensions,
Phys. Rev. E, Vol. 91, art. 032403, 8pp.
V.
The problem of facets:
Issues of boundary conditions for continuum variables at facet edges.
Related papers:
1. D. Margetis, P.-W. Fok, M. J. Aziz, and H. A. Stone (2006),
Continuum theory of nanostructure decay
via a microscale condition
(PDF), Physical Review Letters, Vol. 97, art. 096102, 4pp.
Also selected to appear in the Virtual Journal of Nanoscale
Science & Technology, September 11, 2006
(
http://www.vjnano.org/nano/ ).
2. Margetis, D., and K. Nakamura (2011),
``From crystal steps to continuum laws: behavior near
large facets in one dimension'', Physica D,
Vol. 240, pp. 1100-1110.
3. Nakamura, K., and D. Margetis (2013),
``Discrete and continuum relaxation dynamics of faceted crystal surface in evaporation models'',
(SIAM Journal on) Multiscale Modeling & Simulation, Vol. 11(1), pp. 244-281.
4. Schneider, J. P., K. Nakamura, and D. Margetis (2014),
``Role of chemical potential in relaxation of faceted crystal structure'',
Physical Review E, Vol. 89, 062408 (12pp).
VI.
Radial setting:
Step motion laws versus continuum theory: Theoretical predictions
are derived
using a PDE and comparisons are made with discrete simulations for axisymmetric profiles.
In particular, the issue of boundary conditions at facet edges is addressed.
Related papers:
1. D. Margetis, P.-W. Fok, M. J. Aziz, and H. A. Stone (2006),
Continuum theory of nanostructure decay
via a microscale condition
(PDF), Physical Review Letters, Vol. 97, art. 096102, 4pp.
Also selected to appear in the Virtual Journal of Nanoscale
Science & Technology, September 11, 2006
(
http://www.vjnano.org/nano/ ).
2. D. Margetis, M. J. Aziz, and H. A. Stone (2005),
Continuum approach to self-similarity and scaling in
morphological relaxation
of a crystal with a facet
(PDF), Physical Review B, Vol. 71, art. 165432, 22pp.
3. D. Margetis, M. J. Aziz, and H. A. Stone (2004),
Continuum description of profile scaling in nanostructure decay
(PDF),
Physical Review B (Rapid Communications), Vol. 69, art. 041404(R), 4pp.
VII.
Derivation of
mesoscopic and macroscopic material parameters, such
as step stiffness and permeability, from a
kinetic model of epitaxial
growth; description of out-of-equilibrium kinetics and equilibrium:
1. D. Margetis and R. E. Caflisch (2008),
Anisotropic step stiffness from
a kinetic model of epitaxial growth
(PDF);
Multiscale
Modeling & Simulation, Vol. 7, pp. 242-273.
2. P. N. Patrone,
R. E. Caflisch, and D. Margetis (2012),
``Characterizing equilibrium in epitaxial
growth''
, Europhys. Lett., Vol. 97, art. 48012
(5pp).
3. J. Papac, D. Margetis, F. Gibou, and C. Ratsch (2014),
``Island dynamics model for mound formation: Effect of step-edge barrier'',
Phys. Rev. E, Vol. 90, art. 022404 (8pp).
VIII.
Continuum description of step motion via
continuum Lagrangian coordinates and shocks; study of formation
of step bunches
and evolution of facets.
1. P.-W. Fok, R. R. Rosales, and D. Margetis (2007),
Unification of step bunching phenomena on vicinal surfaces
(PDF),
Physical Review B, Vol. 76, art. 033408, 4pp.
Also selected to appear in the Virtual Journal of Nanoscale
Science & Technology, July 23, 2007
(
http://www.vjnano.org/nano/
).
2. P.-W. Fok, R. R. Rosales, and D. Margetis (2008),
Facet evolution on supported nanostructures: the effect of finite height,
Physical Review B, Vol. 78, 235401, 17pp.
IX.
Elastic step interactions in two space dimensions
by use of geometric perturbations and the Mellin transform technique.
1. Quah, J., L. P. Liang, and D. Margetis (2010),
``Formulas for
force dipole
interaction
of surface line
defects in homoepitaxy'', accepted for publication,
J. Phys. A: Mathematical and Theoretical, Vol. 43, art. 455001,
20pp.
X.
Analytical study of grooving of grain boundaries by evaporation-condensation or surface-diffusion processes
via self-similar shapes below the roughening transition temperature.
1. H. A. Stone, M. J. Aziz, and D. Margetis (2005),
Grooving of a grain boundary by evaporation-condensation below the roughening transition
(PDF);
Journal of Applied Physics, Vol. 97, art. 113535, 6pp.
XI.
Short expository review article on continuum descriptions of crystal surface morphology evolution.
H. A. Stone and D. Margetis (2005),
Continuum descriptions of crystal surface evolution
(PDF);
review article in the book series Handbook of Materials Modeling, Vol. I: Methods and Models,
pp. 1389-1401, S. Yip (Editor), Springer Verlag, Netherlands.








