Welcome to Ben Kedem's Home Page


Lectures at Leuven Boris' art Chesapeake Bay
Professors 2001 Earth lights Typical Israeli Symposium_2009 

Address:
Benjamin Kedem, Professor             Tel: 301-405-5112
Department of Mathematics             Fax: 301-314-0827
University of Maryland                
College Park, Maryland, 20742-4015

Affiliated with the Institute for Systems Research, ISR University Of Maryland,
College Park. See http://www.isr.umd.edu/People/faculty/Kedem.html.

For ISR reports and theses click here.

Go to:

Research Selected Publications RIT Dissertations Random Field Generation Teaching Service Information SCMA 2005

The Impact of the Internet on Our Society:

Economic Impact Social Impact

Research

I have done work in time series analysis, space-time statistical problems, and combination of information from several sources. Some typical terms and relevant references are as follows.

HOC
HOC stands for higher order crossings, a topic discussed here. The idea is to combine zero-crossing counts in stationary time series with linear filters. This leads to an approach to spectral analysis of stationary time series. Early papers are 1. Kedem and Slud, Annals of Statistics, Vol. 10, 786-794, 1982. 2. Kedem, Annals of Statistics, Vol. 12, 665-674, 1984. Later developments include 1. Kedem and Li, Annals of Statistics, Vol. 19, 1672-1676, 1991. 2. Kedem and Slud, Stoch. Proc. and Their Appl., Vol. 49, 227-244. The last paper shows the zero-crossing rate of a Gaussian process in discrete time need not converge to a constant when the spectrum contains jumps.
CM
The Contraction Mapping, CM, method in spectral analysis is an offshoot of HOC, where frequencies of sinusoidal components in noise are estimated by an iterative process. Use is made of parametric filters that are tuned iteratively by observables such as HOC, LS estimates, and the sample ACF. See 1. He and Kedem, IEEE Tr. Inf. Theory, Vol. 35, 360-370, 1989. 2. Yakowitz, IEEE Tr. Inf. Thery, Vol. 37, 1177-1182, 1991. 3. Li and Kedem, J. Mult. Analysis, Vol. 46, 214-236, 1993. 4. Kedem and Troendle, J. Time Series, Vol. 15, 45-63, 1994. 5. Lopes and Kedem, Stoch. Models, Vol. 10, 309-333, 1994. 6. Li and Kedem, J. Time Series, Vol. 19, 69-82, 1998.
Rice Formula
Rice's celebrated formula, due to S.O. Rice, 1944, gives the expected zero-crossing rate of a stationary Gaussian process. A method for obtaining similar explicit formulas for some non-Gaussian processes is described in 1. Barnett and Kedem, IEEE Tr. Inf. Theory, Vol. 37, 1188-1194, 1991. 2. IEEE Tr. Inf. Thery, Vol. 44, 1672-1677, 1998. The last paper shows the formula is not universal.
TM
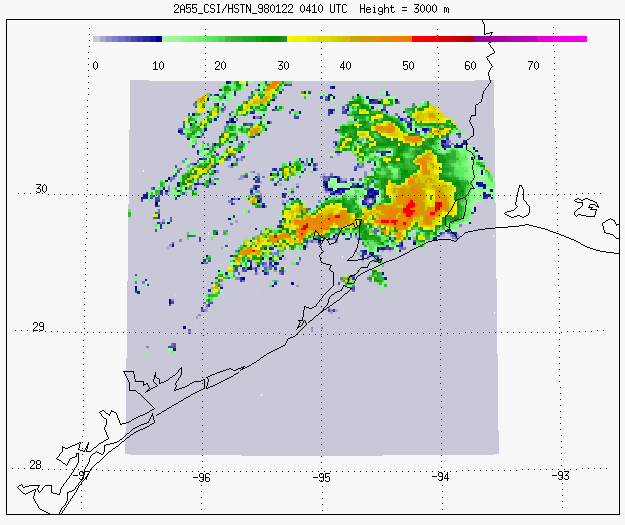
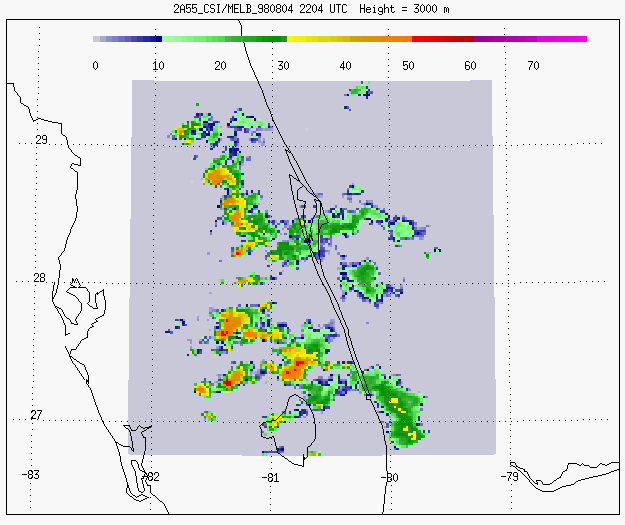
TM stands for "Threshold Method." It is a method whereby an area average is obtained from the fraction of the area that exceeds a fixd threshold. The method has been studied in connection with the Tropical Rainfall Measuring Mission (TRMM). For example, it is possible to obtain the area average in dBZ of the following WSR-88D ground based precipitation radar snapshots (Houston, TX, 01-22-1998, Melbourne, FL, 08-04-1998) from the percent of the dark red area relative to the whole area. See 1. Kedem, Chiu, Karni, J. Appl. Meteor., Vol. 29, 3-20, 1990. 2. Kedem and Pavlopoulos, J. Amer. Statist. Assoc., Vol. 86, 626-633, 1991. 3. Short, Shimizu, Kedem, J. Appl. Meteor., Vol. 32, 182-192, 1993. These papers show optimal thresholds exist under some conditions. See
  • TRMM Satellite,
  • TM_LC,
  • Threshold Method for LN data.

    Houston, TX, 01-22-1998 Melbourne, FL, 08-04-1998
    Thanks are due to Dave Wolff for the snapshot.

    PL
    PL, "partial likelihood", is an idea, due to D.R. Cox, 1975, useful in estimation. Although not a full likelihood, PL enjoys many of the properties of full likelihood but at some efficiency cost. It is a notion particularly useful in time series analysis. See 1. Slud and Kedem, Statistica Sinica, Vol. 4, 89-106, 1994. 2. Fokianos and Kedem, J. Mult. Analysis, Vol. 67, 277-296, 1998. PL was also used in a switching model than can be downloaded by clicking switching model. See SCMA 2005 lecture. See GLM. See RidgeReg See monteCarlo.00 See monteCarlo.11 See monteCarlo.MCMC
    Spatial Prediction (BTG)
    BTG, Bayesian-Transformed-Gaussian, is a method for spatial prediction/interpolation formulated by Victor De Oliveira. See De Oliveira, Kedem, Short, J. Amer. Statist. Assoc., Vol. 92, 1422-1433, 1997. You can download the software (developed by David Bindel) and learn more about the method by clicking BTG or GWU 2009 lecture. Ch_Pred1sld The following is an example of a prediction map obtained by BTG from 24 data points.


    Combination or Fusion of Information
    Consider m distributions where the first m-1 are obtained by multiplicative exponential distortions of the the mth distribution, it being a reference. Given m corresponding samples, the semiparametric large sample problem is worked out regarding the estimation from the combined data of each distortion and the common factor, and testing the hypothesis the distributions are identical. The approach is a generalization of the classical one way layout classification in the general sense it obviates the need for a complete specified parametric model. An advantage is that the common factor, the probability density of the m'th distribution, is estimated from the combined data and not just from the m'th sample. A power comparison with the t and F tests obtained by simulation points to the merit of the present approach. The method is applied to rain rate data from meteorological instruments. See Fokianos, Kedem, Qin, Short, "A semiparametric approach to the one way layout," Technometrics, 2001, Vol. 43, 56-65. Many more results along the same lines can be found in the 2017 book NCSU_2013> "Statistical Data Fusion" by Kedem, De Oliveira, Sverchkov.
    Clipped Gaussian Random Fields
    Clipped Gaussian random fields can be used for modeling discrete-valued random fields with a given correlation structure. If every quantization level is represented by a specific color, then clipping at several levels produces a color map as created by > > Boris Kozintsev, 1999. Note that in "cgi?3" there are 3 colors, in "cgi?9" there are 9 colors, etc. For more information about the online generation of Gaussian random fields and their clipped versions click here.
    • Time Series Regression Models
    The GLM methodology has been extended to time series in "Regression Models for Time Series Analysis", by Kedem and Fokianos, Wiley, 2002. See TimeSeries3.

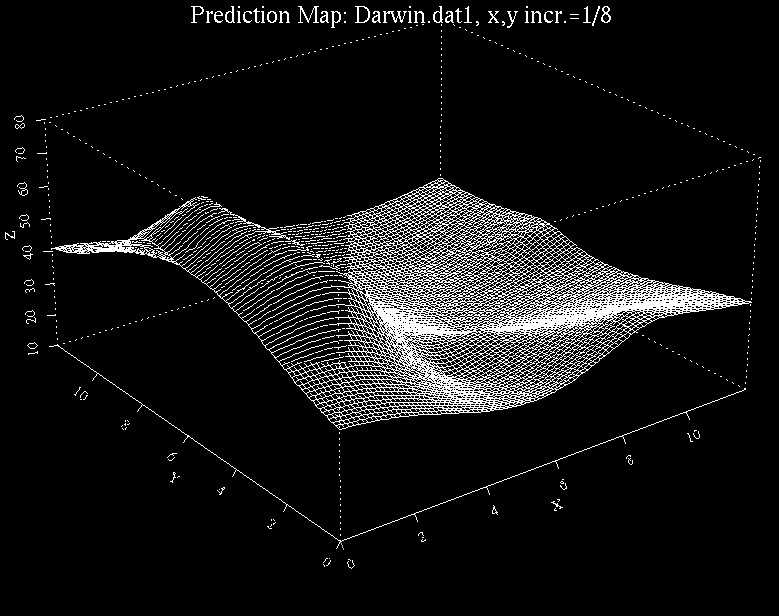
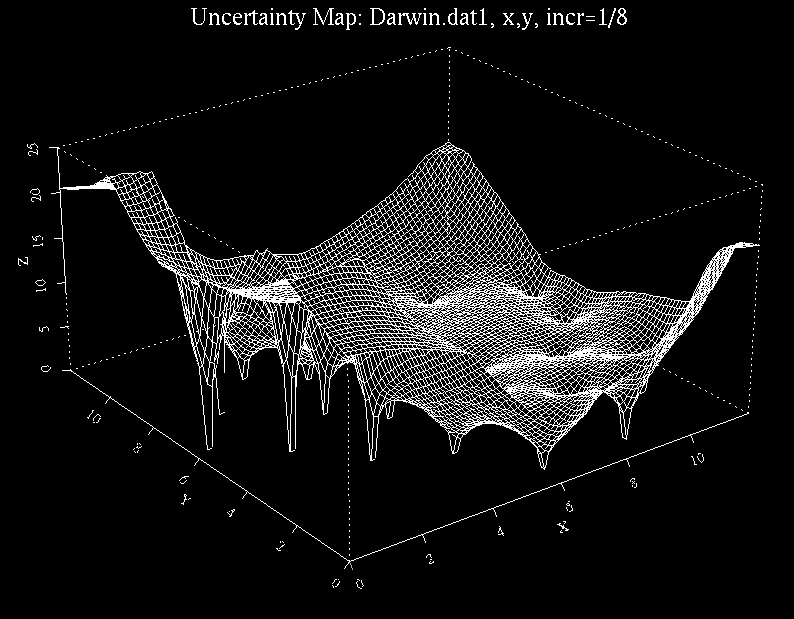
    A stochastic color map representing a scaled clipped (6 levels) version of the 256 by 256 realization on the left. Every category is represented by a color. The 7 colors are magenta, cyan, dark blue, yellow, light green, forest green, and orange. For more information about the online generation of similar images, click on any of them. Estimation of correlation parameters in the original Gaussian random field from clipped images is treated in Kozintsev (1999).


    Some 256 by 256 clipped binary images from an isotropic Gaussian random field with Matern(1,7) correlation,
    PhD Dissertations Directed

    Student Thesis title Year
    George Reed Applications of Higher Order Crossings 1983
    Donald E.K. Martin Estimation of the Minimal Period of Periodically Correlated Sequences 1990
    Silvia R.C. Lopes Spectral Analysis in Frequency Modulated Models 1991
    Haralabos Pavlopoulos Statistical Inference for Optimal Thresholds 1991
    James Troendle An Iterative Filtering Method of Frequency Detection in a Mixed Spectrum Model 1991
    Ta-Hsin Li Estimation of Multiple Sinusoids by Parametric Filtering 1992
    John Barnett Zero-Crossing Rates of Some Non-Gaussian Processes with Application to Detection and Estimation 1996
    Konstantinos Fokianos Categorical Time Series: Prediction and Control 1996
    Victor De Oliveira Prediction in Some Classes of Non-Gaussian Random Fields 1997
    Neal Jeffries Logistic Mixtures of Generalized Linear Model Times Series 1998
    Boris Kozintsev Computations With Gaussian Random Fields 1999
    Richard Gagnon Certain Computational Aspects of Power Efficiency and of State Space Models 2005
    Haiming Guo Generalized Volatility Model and Calculating VaR Using a New Semiparametric Model 2005
    Guanhua Lu Asymptotic Theory for Multiple-Sample Semiparametric Density Ratio Models and its Application to Mortality Forecasting 2007
    Shihua Wen Semi-Parametric Cluster Detection 2007

    Teaching: Spring 2009

    STAT 730: Time Series Analysis
    MWF 2:00 PM
    Syllabus

    A time series is a sequence of observations made on a stochastic process sequentially in ``time''. Examples are economic time series, electronic signals (analog and digital), geophysical time series, random binary sequences, random vibration signals in mechanical systems, and many many more. Time series analysis is concerned with statistical/probabilistic methods for making inference based on sequential data; for example forecasting or prediction and interpolation. Time series analysis is widespread throughout the physical and social sciences, and engineering. Special emphasis will be placed on the use of the Splus software in time series analysis.

    A related area is the analysis of spatial data, for example, geophysical 3D realizations. Prediction or interpolation in spatial data is closely related to that of time series, and in fact the two are almost indistinguishable. More generally, the correlation and spectral theory of stationary spatial data is essentially the same as that of time series.

    In recent years there is a growing interest in regression models for time series tailored after ordinary linear models, except that the data are dependent, a fact that must be taken into account. Interestingly, the fact that time series are sequential is the basic fact that mitigates the problem of dependence under certain regularity conditions.

    For over 40 years state space models have been playing an important role in modeling and forecasting nonstationary time series that follow certain dynamic equations. The use of state space models is widespread in such diverse fields as aerospace engineering and economics. State space models may be viewed as regression models with random coefficients.

    A typical time series displays up and down oscillation. The study of this oscillation can be approached in several ways. In stationary time series this can be accomplished via spectral analysis, and higher order crossings. The expected number of level crossings by a stationary time series is an important problem in structural engineering. The course will cover current topics in time series analysis including:

    Texts:

    Teaching: FALL 2007

    STAT 740: Linear Models I
    Math Building Room 0302, MWF 11:00 AM
    Syllabus

    Linear Models I deals with regression models, linear and non-linear, satisfying various assumptions. The basic idea is to relate a dependent variable to a set of covariates. The course will emphasize the following topics.

    STAT 741: Linear Models II
    Math Building Room 1313, MWF 10:00 AM

    TakeHome Exam, Spring 2007

    Service: Spring 1999

    Service: Spring 2003


    Information

    | ISR Reports | UMD - System | UMD - College Park | Department Directory | Colloquium | |

    Useful Links