NEWS:
- Final Exam
You can bring a cheat sheet: letter size, 2-sided, must be handwritten
topics for final and problems
solutions- Exam 2 was on Monday, Dec. 5.
Solution
corrected version: Topics and practice problems , solutions- Matlab m-files:
- binomial tree model based on YEARLY data: ybinom_eu.m
- Black-Scholes option prices for European call/put options: BlackScholes.m
We can use this to find the implied volatility from call option prices using fzero, see the course notes and the example just below.
To find the implied volatility from put option prices: Use BlackScholesPut.m- Example for using stock and option prices in Matlab, computing implied volatility (m-file)
uses the following m-files (UPDATED version from Oct. 25):
get current option prices: getOptionPrices.m
plot option prices: option_plot.m- Practice problems for Exam 1
solution- Exam 1 is on Mon, Oct. 17
Solution of Exam
It covers the following topics:
- Present Value Analysis (Section 2 in the notes)
write Matlab code to find answer (payment or interest rate)
You may need fzero command.- Probability: expectation, variance, conditional expectation (Sections 3.1-3.10)
- No Arbitrage Principle, Comparison principle (Sections 4.6)
- Option pricing with risk-neutral measure (Sections 4.9,4.10)
- Binomial tree model, trinomial tree model (Sections 4.1,4.2)
- Option pricing algorithm for binomial tree model, Delta hedging (Sections 4.11, Conclusion on p.36, 4.17-4.20)
- Properties of option prices (Section 5)
- Assignment 2 is due on Wed, Oct. 12, 9pm
Solution of problem 1, m-file a2p1ab.m
Solution of problem 2, m-files: xbinom_eu_put.m, xbinom_am_put.m, xbinom_am_call.m
Hand in printouts of all m-files you used (unless they are exactly the m-files which I provided). Use publish in Matlab. I need to see all code and the generated output and graphics.- Option pricing with binomial trees in Matlab (see course notes):
binom_eu.m, binom_am.m, xbinom_eu_call.m- Download the m-file xbinom_eu_call.m. Then run the example from section 4.19 in the class notes:
S0=10; K=11; [V,av] = xbinom_eu_call(.01,S0,1.1,.9,10,K,3);- Course notes (Nov. 2), Appendix: Convex separation theorem
- Solution of Assignment 1, m-file Please look at this solution and make sure that you understand the Matlab code.
In particular look at the Matlab code for "Problem 3(a), Method 2" where I use vectors in Matlab. You will need this for future assignments.- Assignment 1, due Wed Sept. 14 at 9pm
- Use the links below to find the price for an Apple (AAPL) put option and call option with strike price $100 and maturity June 2017.
- If you are not familiar with Matlab do the following NOW:
- Read the "gentle introduction to Matlab" below
- Read the first 10 pages of the Matlab Primer (see below) AND TRY OUT THE COMMANDS ON A COMPUTER.
- Figure out how to write, run, and publish an m-file.
 |
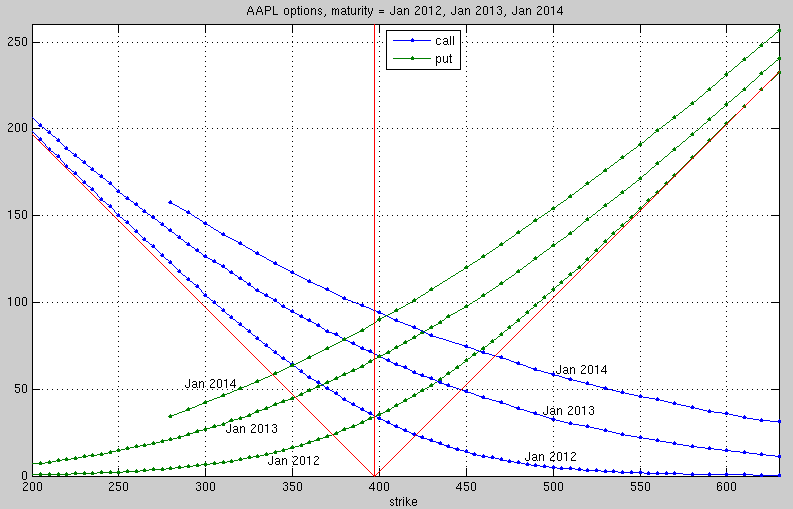
| AAPL option prices in Sept. 2011 for three different maturities |
SYLLABUS: Information about exams, homeworks, grades
[sopen,sclose,shigh,slow,svol] = get_stock('AAPL',[2001 8],2004)Type help get_stock for more information.
We will use Matlab for all computations.
How to hand in Matlab results for homeworks: